
【题目】如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=![]() ,∠BAD=90°.
,∠BAD=90°.
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求异面直线BC与MD所成角的余弦值;
(Ⅲ)求直线CD与平面ABD所成角的正弦值.

【答案】(Ⅰ)证明见解析;(Ⅱ) ![]() ;(Ⅲ)
;(Ⅲ) ![]() .
.
【解析】分析:(Ⅰ)由面面垂直的性质定理可得AD⊥平面ABC,则AD⊥BC.
(Ⅱ)取棱AC的中点N,连接MN,ND.由几何关系可知∠DMN(或其补角)为异面直线BC与MD所成的角.计算可得 .则异面直线BC与MD所成角的余弦值为
.则异面直线BC与MD所成角的余弦值为![]() .
.
(Ⅲ)连接CM.由题意可知CM⊥平面ABD.则∠CDM为直线CD与平面ABD所成的角.计算可得![]() .即直线CD与平面ABD所成角的正弦值为
.即直线CD与平面ABD所成角的正弦值为![]() .
.
详解:(Ⅰ)证明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.
(Ⅱ)取棱AC的中点N,连接MN,ND.又因为M为棱AB的中点,故MN∥BC.所以∠DMN(或其补角)为异面直线BC与MD所成的角.

在Rt△DAM中,AM=1,故DM=![]() .因为AD⊥平面ABC,故AD⊥AC.
.因为AD⊥平面ABC,故AD⊥AC.
在Rt△DAN中,AN=1,故DN=![]() .
.
在等腰三角形DMN中,MN=1,可得 .
.
所以,异面直线BC与MD所成角的余弦值为![]() .
.
(Ⅲ)连接CM.因为△ABC为等边三角形,M为边AB的中点,故CM⊥AB,CM=![]() .又因为平面ABC⊥平面ABD,而CM
.又因为平面ABC⊥平面ABD,而CM![]() 平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角.
平面ABC,故CM⊥平面ABD.所以,∠CDM为直线CD与平面ABD所成的角.
在Rt△CAD中,CD=![]() =4.
=4.
在Rt△CMD中, ![]() .
.
所以,直线CD与平面ABD所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】“H大桥”是某市的交通要道,提高过桥车辆的通行能力可改善整个城市的交通状况.研究表明:在一般情况下,大桥上的车流速度![]() (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度![]() (单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为
(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为![]() ;当车流密度不超过20辆/千米时,车流速度为60千米/小时;当
;当车流密度不超过20辆/千米时,车流速度为60千米/小时;当![]() 时,车流速度
时,车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式.
的表达式.
(2)设车流量![]() ,求当车流密度为多少时,车流量最大?
,求当车流密度为多少时,车流量最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我们把定义域为![]() 且同时满足以下两个条件的函数
且同时满足以下两个条件的函数![]() 称为“
称为“![]() 函数”:(1)对任意的
函数”:(1)对任意的![]() ,总有
,总有![]() ;(2)若
;(2)若![]() ,
,![]() ,则有
,则有![]() 成立,下列判断正确的是( )
成立,下列判断正确的是( )
A.若![]() 为“
为“![]() 函数”,则
函数”,则![]()
B.若![]() 为“
为“![]() 函数”,则
函数”,则![]() 在
在![]() 上为增函数
上为增函数
C.函数![]() 在
在![]() 上是“
上是“![]() 函数”
函数”
D.函数![]() 在
在![]() 上是“
上是“![]() 函数”
函数”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中的一个椭圆,它的中心在原点,左焦点为
中的一个椭圆,它的中心在原点,左焦点为![]() ,右顶点为
,右顶点为![]() ,设点
,设点![]() .
.
(1)求该椭圆的标准方程;
(2)若![]() 是椭圆上的动点,求线段
是椭圆上的动点,求线段![]() 的中点
的中点![]() 的轨迹方程;
的轨迹方程;
(3)过原点![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,求
两点,求![]() 面积的最大值,并求此时直线
面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小张在淘宝网上开一家商店,他以10元每条的价格购进某品牌积压围巾2000条.定价前,小张先搜索了淘宝网上的其它网店,发现:![]() 商店以30元每条的价格销售,平均每日销售量为10条;
商店以30元每条的价格销售,平均每日销售量为10条;![]() 商店以25元每条的价格销售,平均每日销售量为20条.假定这种围巾的销售量
商店以25元每条的价格销售,平均每日销售量为20条.假定这种围巾的销售量![]() (条)是售价
(条)是售价![]() (元)
(元)![]() 的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
的一次函数,且各个商店间的售价、销售量等方面不会互相影响.
(1)试写出围巾销售每日的毛利润![]() (元)关于售价
(元)关于售价![]() (元)
(元)![]() 的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
的函数关系式(不必写出定义域),并帮助小张定价,使得每日的毛利润最高(每日的毛利润为每日卖出商品的进货价与销售价之间的差价);
(2)考虑到这批围巾的管理、仓储等费用为200元/天(只要围巾没有售完,均须支付200元/天,管理、仓储等费用与围巾数量无关),试问小张应该如何定价,使这批围巾的总利润最高(总利润=总毛利润-总管理、仓储等费用)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着雾霾的日益严重,中国部分省份已经实施了“煤改气”的计划来改善空气质量指数.2017年支撑我国天然气市场消费增长的主要资源是国产常规气和进口天然气,资源每年的增量不足以支撑天然气市场连续![]() 亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在
亿立方米的年增量.进口LNG和进口管道气受到接收站、管道能力和进口气价资源的制约.未来,国产常规气产能释放的红利将会逐步减弱,产量增量将维持在![]() 亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续
亿方以内.为了测定某市是否符合实施煤改气计划的标准,某监测站点于2016年8月某日起连续![]() 天监测空气质量指数(AQI),数据统计如下:
天监测空气质量指数(AQI),数据统计如下:
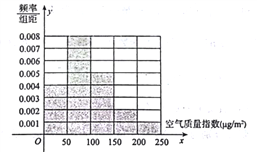
(1)根据上图完成下列表格
空气质量指数( |
|
|
|
|
|
天数 |
(2)计算这![]() 天中,该市空气质量指数的平均数;
天中,该市空气质量指数的平均数;
(3)若按照分层抽样的方法,从空气质量指数在![]() 以及
以及![]() 的等级中抽取
的等级中抽取![]() 天进行调研,再从这
天进行调研,再从这![]() 天中任取
天中任取![]() 天进行空气颗粒物分析,求恰有
天进行空气颗粒物分析,求恰有![]() 天空气质量指数在
天空气质量指数在![]() 上的概率.
上的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() ,
,![]() 时,求满足
时,求满足![]() 的
的![]() 的值;
的值;
(2)若函数![]() 是定义在
是定义在![]() 上的奇函数.
上的奇函数.
①存在![]() ,使得不等式
,使得不等式![]() 有解,求实数
有解,求实数![]() 的取值范围;
的取值范围;
②若函数![]() 满足
满足![]() ,若对任意
,若对任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com