
【题目】某校命制了一套调查问卷(试卷满分均为100分),并对整个学校的学生进行了测试.现从这些学生的成绩中随机抽取了50名学生的成绩,按照![]() 分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).

(1)求频率分布直方图中x的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)用样本估计总体,若该校共有2000名学生,试估计该校这次测试成绩不低于70分的人数;
(3)若利用分层抽样的方法从样本中成绩不低于70分的学生中抽取6人,再从这6人中随机抽取3人,试求成绩在![]() 的学生至少有1人被抽到的概率.
的学生至少有1人被抽到的概率.
【答案】(1)![]() ,74,
,74,![]() ;(2)1200;(3)
;(2)1200;(3)![]() .
.
【解析】
(1)根据频率和为![]() 可求得第第
可求得第第![]() 组的频率,由此求得
组的频率,由此求得![]() 的值;根据频率分布直方图中平均数和中位数的估计方法可计算得到结果;
的值;根据频率分布直方图中平均数和中位数的估计方法可计算得到结果;
(2)计算得到![]() 名学生中成绩不低于
名学生中成绩不低于![]() 分的频率,根据样本估计总体的方法,利用总数
分的频率,根据样本估计总体的方法,利用总数![]() 频率可得所求人数;
频率可得所求人数;
(3)根据分层抽样原则确定![]() 、
、![]() 和
和![]() 种分别抽取的人数,采用列举法列出所有结果,从而可知成绩在
种分别抽取的人数,采用列举法列出所有结果,从而可知成绩在![]() 的学生没人被抽到的概率;根据对立事件概率公式可求得结果.
的学生没人被抽到的概率;根据对立事件概率公式可求得结果.
(1)由频率分布直方图可得第![]() 组的频率为:
组的频率为:![]()
![]()
估计所抽取的![]() 名学生成绩的平均数为:
名学生成绩的平均数为:![]()
由于前两组的频率之和为![]() ,前三组的频率之和为
,前三组的频率之和为![]()
![]() 中位数在第
中位数在第![]() 组中
组中
设中位数为![]() ,则有:
,则有:![]() ,解得:
,解得:![]()
即所求的中位数为![]()
(2)由(1)知:![]() 名学生中成绩不低于
名学生中成绩不低于![]() 分的频率为:
分的频率为:![]()
用样本估计总体,可以估计高三年级![]() 名学生中成绩不低于
名学生中成绩不低于![]() 分的人数为:
分的人数为:![]()
(3)由(1)可知,后三组中的人数分别为![]() ,
,![]() ,
,![]()
![]() 这三组中所抽取的人数分别为
这三组中所抽取的人数分别为![]() ,
,![]() ,
,![]()
记成绩在![]() 的
的![]() 名学生分别为
名学生分别为![]() ,成绩在
,成绩在![]() 的
的![]() 名学生分别为
名学生分别为![]() ,成绩在
,成绩在![]() 的
的![]() 名学生为
名学生为![]() ,则从中随机抽取
,则从中随机抽取![]() 人的所有可能结果为:
人的所有可能结果为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共
,共![]() 种
种
其中成绩在![]() 的学生没人被抽到的可能结果为
的学生没人被抽到的可能结果为![]() ,只有
,只有![]() 种,
种,
故成绩在![]() 的学生至少有
的学生至少有![]() 人被抽到的概率:
人被抽到的概率:![]()


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() 是以坐标原点
是以坐标原点![]() 为顶点,直线
为顶点,直线![]() 为准线的抛物线.以坐标原点
为准线的抛物线.以坐标原点![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立极坐标系.
轴非负半轴为极轴建立极坐标系.
(1)分别求出直线![]() 与曲线
与曲线![]() 的极坐标方程:
的极坐标方程:
(2)点![]() 是曲线
是曲线![]() 上位于第一象限内的一个动点,点
上位于第一象限内的一个动点,点![]() 是直线
是直线![]() 上位于第二象限内的一个动点,且
上位于第二象限内的一个动点,且![]() ,请求出
,请求出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,圆锥的顶点为A,底面的圆心为O,BC是底面圆的一条直径,点D,E在底面圆上,已知![]() ,
,![]() .
.
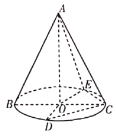
(1)证明:![]() ;
;
(2)若二面角![]() 的大小为
的大小为![]() ,求直线OC与平面ACE所成角的正弦值.
,求直线OC与平面ACE所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市为了解顾客的购物量及结算时间等信息,安排一名员工随机收集了在该超市购物的100位顾客的相关数据,统计结果如下表所示,已知这100位顾客中一次购物量超过7件的顾客占![]() .
.
一次购物量 | 1至3件 | 4至7件 | 8至11件 | 12至15件 | 16件及以上 |
顾客数(人) |
| 27 | 20 |
| 10 |
结算时间( | 0.5 | 1 | 1.5 | 2 | 2.5 |
(1)确定![]() ,
,![]() 的值,并求顾客一次购物的结算时间的平均值;
的值,并求顾客一次购物的结算时间的平均值;
(2)从收集的结算时间不超过![]() 的顾客中,按分层抽样的方法抽取5人,再从这5人中随机抽取2人,求至少有1人的结算时间为
的顾客中,按分层抽样的方法抽取5人,再从这5人中随机抽取2人,求至少有1人的结算时间为![]() 的概率.(注:将频率视为概率)
的概率.(注:将频率视为概率)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
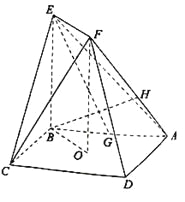
(Ⅰ)求证:EG∥平面ADF;
(Ⅱ)求二面角OEFC的正弦值;
(Ⅲ)设H为线段AF上的点,且AH=![]() HF,求直线BH和平面CEF所成角的正弦值.
HF,求直线BH和平面CEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某部队在一次军演中要先后执行六项不同的任务,要求是:任务![]() 必须排在前三项执行,且执行任务
必须排在前三项执行,且执行任务![]() 之后需立即执行任务
之后需立即执行任务![]() ,任务
,任务![]() 、
、![]() 相邻,则不同的执行方案共有______种.
相邻,则不同的执行方案共有______种.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,过
,过![]() 作倾斜角互补的两条不同直线
作倾斜角互补的两条不同直线![]() 、
、![]() .
.

(1)求抛物线![]() 的方程及准线方程;
的方程及准线方程;
(2)设直线![]() 、
、![]() 分别交抛物线
分别交抛物线![]() 于
于![]() 、
、![]() 两点(均不与
两点(均不与![]() 重合,如图),记直线
重合,如图),记直线![]() 的斜率为正数
的斜率为正数![]() ,若以线段
,若以线段![]() 为直径的圆与抛物线的准线相切,求
为直径的圆与抛物线的准线相切,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com