
思路分析:因为总体共有彩电5 000台,数量较大,所以不宜采用简单随机抽样.又由于三种彩电的进货数量差异较大,故也不宜用系统抽样的方法,而用分层抽样为妥.
解:在随机抽取的60台彩电中:“康佳”彩电的数量应为![]() ×60=38台;“海信”彩电的数量应为
×60=38台;“海信”彩电的数量应为![]() ×60=16台;“熊猫”彩电的数量应为
×60=16台;“熊猫”彩电的数量应为![]() ×60=6台.
×60=6台.
因此在3 000×![]() =1 900台“康佳”彩电中采用系统抽样法抽取38台:将1 900台“康佳”彩电编号0001—1900,从0001号开始顺次每50个一组,等分成38组,从1—50个数中随机选取1个,再将编号为这个数加上50的倍数的彩电抽取出来.
=1 900台“康佳”彩电中采用系统抽样法抽取38台:将1 900台“康佳”彩电编号0001—1900,从0001号开始顺次每50个一组,等分成38组,从1—50个数中随机选取1个,再将编号为这个数加上50的倍数的彩电抽取出来.
类似地可从3 000×![]() =800台“海信”彩电中采用系统抽样的方法抽取16台,从3 000×
=800台“海信”彩电中采用系统抽样的方法抽取16台,从3 000×![]() =300台“熊猫”彩电中采用系统抽样的方法抽取6台.
=300台“熊猫”彩电中采用系统抽样的方法抽取6台.
如果商场进的货是“康佳”“长虹”和“TCL”彩电,因为三者所占的市场份额差异不大,因此可以采用系统抽样的方法.
首先将3 000×![]() ≈1 056台“康佳”彩电顺次编号0001—1056,将3 000×
≈1 056台“康佳”彩电顺次编号0001—1056,将3 000×![]() =1 000台“长虹”彩电顺次编号1057—2056,将3 000×
=1 000台“长虹”彩电顺次编号1057—2056,将3 000×![]() ≈944台“TCL”彩电顺次编号为2057—3000.
≈944台“TCL”彩电顺次编号为2057—3000.
然后,将号码0001—3000从0 001开始顺次每50个一组,共分成60组.
最后,从1~50个数中随机抽取1个,再将编号为这个数加上50的倍数的彩电共60台抽取出来,作为售后服务跟踪调查对象.
巧解提示 抽样方法的实质是:在抽样过程中,每个个体被抽取的概率相等,并且抽样者对总体结构有一定的了解.本题考查系统抽样的有关概念,系统抽样适用于个体较多但均衡的总体.判断是否为系统抽样(简单随机抽样和分层抽样也是这样),应首先看能否在抽样前知道总体是由什么构成的,抽样的方法能否保证每个个体按事先规定的概率入样(即等可能抽样),再看能否将总体分成几个均衡的部分.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
| 年份(x) | 1 | 2 | 3 | 4 | 5 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 |
 |
| y |
 |
| b |
 |
| a |
 |
| b |
| |||||||
|
 |
| a |
. |
| y |
. |
| x |
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二上学期期中考试理科数学试卷(解析版) 题型:解答题
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
|
年份(x) |
1 |
2 |
3 |
4 |
5 |
|
人数(y) |
3 |
5 |
8 |
11 |
13 |
(1)从这5年中随机抽取两年,求考入大学的人数至少有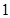 年多于10人的概率.
年多于10人的概率.
(2)根据这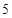 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出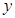 关于
关于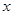 的回归方程
的回归方程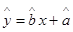 ,并计算第
,并计算第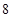 年的估计值。
年的估计值。
参考:用最小二乘法求线性回归方程系数公式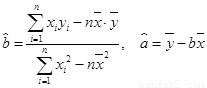
查看答案和解析>>
科目:高中数学 来源:2015届湖北省高二上学期期中考试文科数学试卷(解析版) 题型:解答题
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
|
年份(x) |
1 |
2 |
3 |
4 |
5 |
|
人数(y) |
3 |
5 |
8 |
11 |
13 |
(1)从这5年中随机抽取两年,求考入大学的人数至少有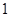 年多于10人的概率.
年多于10人的概率.
(2)根据这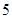 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出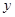 关于
关于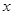 的回归方程
的回归方程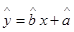 ,并计算第
,并计算第 年的估计值。
年的估计值。
参考:用最小二乘法求线性回归方程系数公式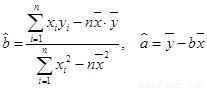
查看答案和解析>>
科目:高中数学 来源: 题型:
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村2001到2005年五年间每年考入大学的人数,为了方便计算,2001年编号为1,2002年编号为2,……,2005年编号为5,数据如下:
| 年份(x) | 1 | 2 | 3 | 4 | 5 |
| 人数(y) | 3 | 5 | 8 | 11 | 13 |
(1)从这5年中随机抽取两年,求考入大学的人数至少有![]() 年多于10人的概率.
年多于10人的概率.
(2)根据这![]() 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出![]() 关于
关于![]() 的回归方程
的回归方程![]() ,并计算第
,并计算第![]() 年的估计值。
年的估计值。
参考:用最小二乘法求线性回归方程系数公式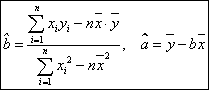
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com