
【题目】若集合![]() 的子集A中的每个元素均可表为两个自然数(允许相同)的平方和,求集合A中元素个数的最大值.
的子集A中的每个元素均可表为两个自然数(允许相同)的平方和,求集合A中元素个数的最大值.
【答案】79
【解析】
注意到,不超过200的平方数为![]() .
.
首先,![]() 中的每个数
中的每个数![]() 可表为
可表为![]() 的形式,这种数共有14个;
的形式,这种数共有14个;
而![]() 中的每一对数(允许相同)的和在集合M中,这种数有
中的每一对数(允许相同)的和在集合M中,这种数有![]() 个,
个,
其中,![]() 形式的数10个,
形式的数10个,![]()
![]()
![]() 形式的数
形式的数![]() 个.
个.
其次,![]() 形式的数8个,
形式的数8个,
![]() 形式的数7个,
形式的数7个,
![]() 形式的数5个,
形式的数5个,
![]() 形式的数2个,
形式的数2个,
共计22个.
再考虑重复的情形:注意到,若![]() ,
,
则![]() .
.
不超过40且能表示为两个不同正整数的平方和的数有5、10、13、17、20、25、26、29、34、37、40,
该组中的每个数与5的积,以及![]() 均在集合M中,且均可用两种方式表示为平方和,
均在集合M中,且均可用两种方式表示为平方和,
故各被计算了两次,累计有12次重复(10、13、17、20与10的积已包含在以上乘积组中).
因此,集合A中元素个数的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】图1是由矩形![]() 和菱形
和菱形![]() 组成的一个平面图形,其中
组成的一个平面图形,其中![]() ,
, ![]() ,将其沿
,将其沿![]() 折起使得
折起使得![]() 与
与![]() 重合,连结
重合,连结![]() ,如图2.
,如图2.
(1)证明图2中的![]() 四点共面,且平面
四点共面,且平面![]() 平面
平面![]() ;
;
(2)求图2中的四边形![]() 的面积.
的面积.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的有( )
①在回归分析中,可以借助散点图判断两个变量是否呈线性相关关系.
②在回归分析中,可以通过残差图发现原始数据中的可疑数据,残差平方和越小,模型的拟合效果越好.
③在回归分析模型中,相关系数的绝对值越大,说明模型的拟合效果越好.
④在回归直线方程![]() 中,当解释变量
中,当解释变量![]() 每增加1个单位时,预报变量
每增加1个单位时,预报变量![]() 增加0.1个单位.
增加0.1个单位.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015年推出一种新型家用轿车,购买时费用为16.9万元,每年应交付保险费、养路费及汽油费共1.2万元,汽车的维修费为:第一年无维修费用,第二年为0.2万元,从第三年起,每年的维修费均比上一年增加0.2万元.
(I)设该辆轿车使用n年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为f(n),求f(n)的表达式;
(II)这种汽车使用多少报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前n项和为
的前n项和为![]() ,且满足
,且满足![]() ,数列
,数列![]() 中,
中,![]() ,对任意正整数
,对任意正整数![]() ,
,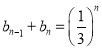 .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比q的值,若不存在,请说明理由;
及公比q的值,若不存在,请说明理由;
(3)求数列![]() 前n项和
前n项和![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆C的标准方程;
(2)点P是椭圆上异于短轴端点A,B的任意一点,过点P作![]() 轴于Q,线段PQ的中点为M.直线AM与直线
轴于Q,线段PQ的中点为M.直线AM与直线![]() 交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.
交于点N,D为线段BN的中点,设O为坐标原点,试判断以OD为直径的圆与点M的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com