
【题目】已知抛物线C1:x2=y,圆C2:x2+(y﹣4)2=1的圆心为点M
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.

【答案】(1)![]() (2)
(2)![]()
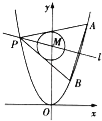
【解析】(1)由题意画出简图为:
由于抛物线C1:x2=y准线方程为:y=﹣![]() ,圆C2:x2+(y﹣4)2=1的圆心M(0,4),
,圆C2:x2+(y﹣4)2=1的圆心M(0,4),
利用点到直线的距离公式可以得到距离d=![]() =
=![]() .
.
(2)设点P(x0,x02),A(x1,x12),B(x2,x22);
由题意得:x0≠0,x2≠±1,x1≠x2,
设过点P的圆c2的切线方程为:y﹣x02=k(x﹣x0)即y=kx﹣kx0+x02①
则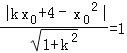 ,即(x02﹣1)k2+2x0(4﹣x02)k+(x02﹣4)2﹣1=0
,即(x02﹣1)k2+2x0(4﹣x02)k+(x02﹣4)2﹣1=0
设PA,PB的斜率为k1,k2(k1≠k2),则k1,k2应该为上述方程的两个根,
∴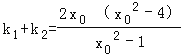 ,
,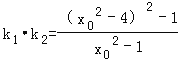 ;
;
代入①得:x2﹣kx+kx0﹣x02="0" 则x1,x2应为此方程的两个根,
故x1=k1﹣x0,x2=k2﹣x0
∴kAB=x1+x2=k1+k2﹣2x0=
由于MP⊥AB,∴kABKMP=﹣1![]()
故P![]() ∴
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】从某山区养殖场散养的3500头猪中随机抽取5头,测量猪的体长x(cm)和体重y(kg),得如下测量数据:
猪编号 | 1 | 2 | 3 | 4 | 5 |
x | 169 | 181 | 166 | 185 | 180 |
y | 95 | 100 | 97 | 103 | 101 |
(1)当且仅当x,y满足:x≥180且y≥100时,该猪为优等品,用上述样本数据估计山区养殖场散养的3500头猪中优等品的数量;
(2)从抽取的上述5头猪中,随机抽取2头中优等品数x的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某保险的基本保费为a(单位:元),继续购买该保险的投保人成为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
设该险种一续保人一年内出险次数与相应概率如下:
一年内出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
概率 | 0.30 | 0.15 | 0.20 | 0.20 | 0.10 | 0.05 |
(1)求一续保人本年度的保费高于基本保费的概率;
(2)若一续保人本年度的保费高于基本保费,求其保费比基本保费高出60%的概率;
(3)求续保人本年度的平均保费与基本保费的比值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某广场中间有一块边长为2百米的菱形状绿化区ABCD,其中BMN是半径为1百米的扇形,∠ABC= ![]() .管理部门欲在该地从M到D修建小路:在
.管理部门欲在该地从M到D修建小路:在 ![]() 上选一点P(异于M,N两点),过点P修建与BC平行的小路PQ.
上选一点P(异于M,N两点),过点P修建与BC平行的小路PQ. 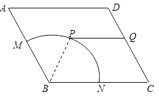
(1)若∠PBC= ![]() ,求PQ的长度;
,求PQ的长度;
(2)当点P选择在何处时,才能使得修建的小路 ![]() 与PQ及QD的总长最小?并说明理由.
与PQ及QD的总长最小?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知整数n≥4,集合M={1,2,3,…,n}的所有含有4个元素的子集记为A1 , A2 , A3 , …, ![]() .
.
设A1 , A2 , A3 , …, ![]() 中所有元素之和为Sn .
中所有元素之和为Sn .
(1)求S4 , S5 , S6并求出Sn;
(2)证明:S4+S5+…+Sn=10Cn+26 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 ![]() ,
, ![]() 是非零不共线的向量,设
是非零不共线的向量,设 ![]() =
= ![]()
![]() +
+ ![]()
![]() ,定义点集M={K|
,定义点集M={K| ![]() =
= ![]() },当K1 , K2∈M时,若对于任意的r≥2,不等式|
},当K1 , K2∈M时,若对于任意的r≥2,不等式| ![]() |≤c|
|≤c| ![]() |恒成立,则实数c的最小值为 .
|恒成立,则实数c的最小值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() +
+ ![]() =1,圆C2:x2+y2=t经过椭圆C1的焦点.
=1,圆C2:x2+y2=t经过椭圆C1的焦点.
(1)设P为椭圆上任意一点,过点P作圆C2的切线,切点为Q,求△POQ面积的取值范围,其中O为坐标原点;
(2)过点M(﹣1,0)的直线l与曲线C1 , C2自上而下依次交于点A,B,C,D,若|AB|=|CD|,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com