
【题目】如图,某广场中间有一块边长为2百米的菱形状绿化区ABCD,其中BMN是半径为1百米的扇形,∠ABC= ![]() .管理部门欲在该地从M到D修建小路:在
.管理部门欲在该地从M到D修建小路:在 ![]() 上选一点P(异于M,N两点),过点P修建与BC平行的小路PQ.
上选一点P(异于M,N两点),过点P修建与BC平行的小路PQ. 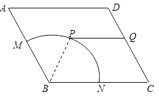
(1)若∠PBC= ![]() ,求PQ的长度;
,求PQ的长度;
(2)当点P选择在何处时,才能使得修建的小路 ![]() 与PQ及QD的总长最小?并说明理由.
与PQ及QD的总长最小?并说明理由.
【答案】
(1)解.如图示:
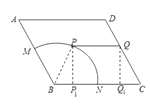 ,
,
连接BP,过P作PP1⊥BC,垂足为P1,过Q作QQ1⊥BC垂足为Q1,
在Rt△PBP1中, ![]() ,PQ=1
,PQ=1
(2)解.设∠PBP1=θ, ![]() ,
,
∴ ![]() ,
,
在Rt△QBQ1中, ![]() ,
,
∴总路径长f(θ)= ![]() ﹣θ+4﹣cosθ﹣
﹣θ+4﹣cosθ﹣ ![]() sinθ,(0<θ<
sinθ,(0<θ< ![]() ),
),
f′(θ)=sinθ﹣ ![]() cosθ﹣1=2sin(θ﹣
cosθ﹣1=2sin(θ﹣ ![]() )﹣1,
)﹣1,
令f'(θ)=0, ![]() ,
,
当 ![]() 时,f'(θ)<0,
时,f'(θ)<0,
当 ![]() 时,f'(θ)>0,
时,f'(θ)>0,
所以当 ![]() 时,总路径最短.
时,总路径最短.
答:当BP⊥BC时,总路径最短
【解析】(1)作出辅助线,根据梯形的性质求出PQ的长即可;(2)设∠PBP1=θ,求出PQ的长,得到总路径长f(θ)的表达式,通过求导得到函数的单调性,从而求出去最小值时θ的值,即P点的位置即可.


科目:高中数学 来源: 题型:
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线与椭圆交于不同的两点
的直线与椭圆交于不同的两点![]() 、
、![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A,B,C,D为平面四边形ABCD的四个内角. 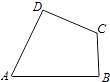
(1)证明:tan ![]() =
= ![]() ;
;
(2)若A+C=180°,AB=6,BC=3,CD=4,AD=5,求tan ![]() +tan
+tan ![]() +tan
+tan ![]() +tan
+tan ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若f(x)=x﹣1﹣alnx,g(x)= ![]() ,a<0,且对任意x1 , x2∈[3,4](x1≠x2),|f(x1)﹣f(x2)|<|
,a<0,且对任意x1 , x2∈[3,4](x1≠x2),|f(x1)﹣f(x2)|<| ![]() ﹣
﹣ ![]() |的恒成立,则实数a的取值范围为 .
|的恒成立,则实数a的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C:y2=2x﹣4.
(1)求曲线C在点A(3, ![]() )处的切线方程;
)处的切线方程;
(2)过原点O作直线l与曲线C交于A,B两不同点,求线段AB的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C1:x2=y,圆C2:x2+(y﹣4)2=1的圆心为点M
(1)求点M到抛物线C1的准线的距离;
(2)已知点P是抛物线C1上一点(异于原点),过点P作圆C2的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的各项均为正数.若对任意的n∈N* , 存在k∈N* , 使得an+k2=anan+2k成立,则称数列{an}为“Jk型”数列.
(1)若数列{an}是“J2型”数列,且a2=8,a8=1,求a2n;
(2)若数列{an}既是“J3型”数列,又是“J4型”数列,证明:数列{an}是等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形![]() 是边长为1的正方形,点
是边长为1的正方形,点![]() 、
、![]() 、
、![]() 、
、![]() 顺次在边
顺次在边![]() 、
、![]() 、
、![]() 、
、![]() 上,且
上,且![]() .过点
.过点![]() 、
、![]() 、
、![]() 、
、![]() 分别作射线
分别作射线![]() 、
、![]() 、
、![]() 、
、![]() ,且
,且![]() ,这里
,这里![]() 为定角,且
为定角,且![]() ,由此得到四边形
,由此得到四边形![]() .
.

(1)问四边形![]() 是怎样的四边形?证明你的结论.
是怎样的四边形?证明你的结论.
(2)设![]() ,试将
,试将![]() 表示成
表示成![]() 的函数.
的函数.
(3)是否存在![]() ,使
,使![]() 为与
为与![]() 无关的定值?若存在,求出相应的
无关的定值?若存在,求出相应的![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com