
【题目】如图所示,![]() 是村里一个小湖的一角,其中
是村里一个小湖的一角,其中![]() . 为了给村民营造丰富的休闲环境,村委会决定在直线湖岸
. 为了给村民营造丰富的休闲环境,村委会决定在直线湖岸![]() 与
与![]() 上分别建观光长廊
上分别建观光长廊![]() 与
与![]() ,其中
,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米;
元/米;![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米;两段长廊的总造价预算为
元/米;两段长廊的总造价预算为![]() 万元(恰好都用完);同时,在线段
万元(恰好都用完);同时,在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个表演舞台,并建水上通道
处建一个表演舞台,并建水上通道![]() (表演舞台的大小忽略不计),水上通道的造价是
(表演舞台的大小忽略不计),水上通道的造价是![]() 元/米.
元/米.

(1)若规划宽长廊![]() 与窄长廊
与窄长廊![]() 的长度相等,则水上通道
的长度相等,则水上通道![]() 的总造价需多少万元?
的总造价需多少万元?
(2)如何设计才能使得水上通道![]() 的总造价最低?最低总造价是多少万元?
的总造价最低?最低总造价是多少万元?
【答案】(1)水上通道AD的总造价为![]() 万元;
万元;
【解析】
试题分析:
(1)设AB=AC=x(单位:百米),由题意可得12x=12,即x=1,求得BD,在![]() 中,由余弦定理求得AD的长,即可得到所求造价;(2)设AB=x,AC=y(单位:百米),则两段长廊的总造价为
中,由余弦定理求得AD的长,即可得到所求造价;(2)设AB=x,AC=y(单位:百米),则两段长廊的总造价为![]() ,运用余弦定理求得BC,再在
,运用余弦定理求得BC,再在![]() 与
与![]() 中,由余弦定理及
中,由余弦定理及![]() ,求得
,求得![]() 的解析式,化简整理,运用配方,即可得到所求最小值,及x,y的值;也可用坐标求解.
的解析式,化简整理,运用配方,即可得到所求最小值,及x,y的值;也可用坐标求解.
试题解析:
(1)设AB=AC=x(单位:百米),则宽长廊AB造价为8x万元,窄长廊AC造价为4x 万元,
故两段长廊的总造价为12x万元,所以12x=12,得x=1,
又![]() ,
,
![]() 是边长为1的正三角形,
是边长为1的正三角形,
又点D为线段BC上靠近点B的三等分点,所以![]() ,
,
在![]() 中,由余弦定理得
中,由余弦定理得
 ,
,
![]() ,
,
又水上通道的造价是6万元/百米,所以水上通道的总造价为![]() 万元.
万元.
(2)法一:设AB=x,AC=y(单位:百米),
则两段长廊的总造价为![]() ,
,
即![]() ,在
,在![]() 中,由余弦定理得
中,由余弦定理得

在![]() 与
与![]() 中,由余弦定理及
中,由余弦定理及![]() ,得
,得
![]() ,
,
又![]() ,得
,得

当且仅当![]() 时,AD有最小值
时,AD有最小值![]() ,
,
故总造价有最小值![]() 万元,此时
万元,此时![]() ,
,
即当宽长廊AB为![]() 百米(75米)、窄长廊AC为
百米(75米)、窄长廊AC为![]() 百米(150米)时,
百米(150米)时,
所以水上通道AD有最低总造价为![]() 万元.
万元.
法二:由![]() ,平方得
,平方得![]() ,以下略.
,以下略.
法三:以A为原点,AP为x轴建立平面直角坐标系,
求出D的坐标得![]() ,以下略.
,以下略.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】现从80瓶水中抽取6瓶进行检验,利用随机数表抽取样本时,先将80瓶水编号,可以编为00,01,02,……,79,在随机数表中任选一个数,例如选出第6行第5列的数7(下面摘取了附表1的第6行至第10行)。
16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 64
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
57 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28
规定从选定的数7开始向右读, 依次得到的样本为__________________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂家拟在2016 年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)![]() 万件与年促销费用
万件与年促销费用![]() 万元(
万元(![]() )满足
)满足![]() 为常数),如果不搞促销活动,则该产品的年销售只能是
为常数),如果不搞促销活动,则该产品的年销售只能是![]() 万件.已知2016 年生产该产品的固定投入为
万件.已知2016 年生产该产品的固定投入为![]() 万元.每生产
万元.每生产![]() 万件该产品需要再投入
万件该产品需要再投入![]() 万元,厂家将每件产品的销售价格定为每件产品年平均成本的
万元,厂家将每件产品的销售价格定为每件产品年平均成本的![]() 倍(产品成本包括固定投入和再投入两部分资金).
倍(产品成本包括固定投入和再投入两部分资金).
(1)将2016 年该产品的利润![]() 万元表示为年促销费用
万元表示为年促销费用![]() 万元的函数;
万元的函数;
(2)该厂家2016 年的促销费用投入多少万元时,厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其指标值来衡量,其指标值越大表明质量越好,且指标值大于或等于102的产品为优质品.现用两种新配方(分别称为![]() 配方和
配方和![]() 配方)做试验,各生产了100件这种产品,并测量了每件产品的指标值,得到了下面的试验结果:
配方)做试验,各生产了100件这种产品,并测量了每件产品的指标值,得到了下面的试验结果:
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 8 | 20 | 42 | 22 | 8 |
![]() 配方的频数分布表
配方的频数分布表
指标值分组 |
|
|
|
|
|
频数 | 4 | 12 | 42 | 32 | 10 |
(Ⅰ)分别估计用![]() 配方,
配方,![]() 配方生产的产品的优质品率;
配方生产的产品的优质品率;
(Ⅱ)已知用![]() 配方生产的一件产品的利润
配方生产的一件产品的利润![]() (单位:元)与其指标值
(单位:元)与其指标值![]() 的关系式为
的关系式为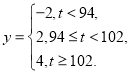
估计用![]() 配方生产的一件产品的利润大于0的概率,并求用
配方生产的一件产品的利润大于0的概率,并求用![]() 配方生产的上述产品平均每件的利润。
配方生产的上述产品平均每件的利润。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某大学一年级女生中,选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名,其身高和体重数据如表所示:
身高/cm ( | 150 | 155 | 160 | 165 | 170 |
体重/kg ( | 43 | 46 | 49 | 51 | 56 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,计算身高为168cm时,体重的估计值![]() 为多少?
为多少?
参考公式:线性回归方程![]() ,其中
,其中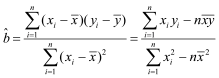 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】尧盛机械生产厂每生产某产品![]() (百台),其总成本为
(百台),其总成本为![]() (万元),其中固定成本为
(万元),其中固定成本为![]() 万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入
万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本).销售收入![]() (万元)满足
(万元)满足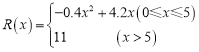 ,假定生产的产品都能卖掉,请完成下列问题:
,假定生产的产品都能卖掉,请完成下列问题:
(1)写出利润函数![]() 的解析式(注:利润=销售收入-总成本);
的解析式(注:利润=销售收入-总成本);
(2)试问该工厂生产多少台产品时,可使盈利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com