
【题目】从某大学一年级女生中,选取身高分别是150cm、155cm、160cm、165cm、170cm的学生各一名,其身高和体重数据如表所示:
身高/cm ( | 150 | 155 | 160 | 165 | 170 |
体重/kg ( | 43 | 46 | 49 | 51 | 56 |
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,计算身高为168cm时,体重的估计值![]() 为多少?
为多少?
参考公式:线性回归方程![]() ,其中
,其中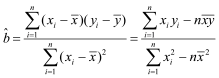 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】下列说法不正确的是( )
A. 圆柱的侧面展开图是一个矩形
B. 圆锥过轴的截面是一个等腰三角形
C. 平行于圆台底面的平面截圆台,截面是圆面
D. 直角三角形绕它的一边旋转一周形成的曲面围成的几何体是圆锥
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 若函数
若函数![]() 的图象与
的图象与![]() 轴相邻两个交点间的距离为
轴相邻两个交点间的距离为![]() ,且图像的一条对称轴是直线
,且图像的一条对称轴是直线![]() 。
。
(1)求![]() 的值;
的值;
(2)求函数![]() 的单调增区间;
的单调增区间;
(3)画出函数![]() 在区间
在区间![]() 上的图像。
上的图像。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是公比为正整数的等比数列,
是公比为正整数的等比数列,![]() 是等差数列,且
是等差数列,且![]() ,
,![]() ,
,![]() .
.
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)设 数列
数列![]() 的前
的前![]() 项和为
项和为![]() .
.
①试求最小的正整数![]() ,使得当
,使得当![]() 时,都有
时,都有![]() 成立;
成立;
②是否存在正整数![]()
![]() ,使得
,使得![]() 成立?若存在,请求出所有满足条件的
成立?若存在,请求出所有满足条件的![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是村里一个小湖的一角,其中
是村里一个小湖的一角,其中![]() . 为了给村民营造丰富的休闲环境,村委会决定在直线湖岸
. 为了给村民营造丰富的休闲环境,村委会决定在直线湖岸![]() 与
与![]() 上分别建观光长廊
上分别建观光长廊![]() 与
与![]() ,其中
,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米;
元/米;![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米;两段长廊的总造价预算为
元/米;两段长廊的总造价预算为![]() 万元(恰好都用完);同时,在线段
万元(恰好都用完);同时,在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个表演舞台,并建水上通道
处建一个表演舞台,并建水上通道![]() (表演舞台的大小忽略不计),水上通道的造价是
(表演舞台的大小忽略不计),水上通道的造价是![]() 元/米.
元/米.

(1)若规划宽长廊![]() 与窄长廊
与窄长廊![]() 的长度相等,则水上通道
的长度相等,则水上通道![]() 的总造价需多少万元?
的总造价需多少万元?
(2)如何设计才能使得水上通道![]() 的总造价最低?最低总造价是多少万元?
的总造价最低?最低总造价是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.

(1)若某位顾客消费128元,求返券金额不低于30元的概率;
(2)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为![]() (元).求随机变量
(元).求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com