
【题目】已知△ABC的内角A,B,C的对边分别为a,b,c,且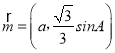 ,
,![]() ,
,![]() .
.
(1)求角A的大小;
(2)若a=3,求△ABC的周长L的取值范围.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】下图为某地区2006年~2018年地方财政预算内收入、城乡居民储蓄年末余额折线图.根据该折线图可知,该地区2006年~2018年( )

A.财政预算内收入、城乡居民储蓄年末余额均呈增长趋势
B.财政预算内收入、城乡居民储蓄年末余额的逐年增长速度相同
C.财政预算内收入年平均增长量高于城乡居民储蓄年末余额年平均增长量
D.城乡居民储蓄年末余额与财政预算内收入的差额逐年增大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() 的值域为
的值域为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在这祥的实数
,是否存在这祥的实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 内有且只有一个零点.若存在,求出
内有且只有一个零点.若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 的左右顶点分别为
的左右顶点分别为![]() .直线
.直线![]() 和两条渐近线交于点
和两条渐近线交于点![]() ,点
,点![]() 在第一象限且
在第一象限且![]() ,
,![]() 是双曲线上的任意一点.
是双曲线上的任意一点.
(1)求双曲线的标准方程;
(2)是否存在点P使得![]() 为直角三角形?若存在,求出点P的个数;
为直角三角形?若存在,求出点P的个数;
(3)直线![]() 与直线
与直线![]() 分别交于点
分别交于点![]() ,证明:以
,证明:以![]() 为直径的圆必过定点.
为直径的圆必过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高二丈,问:积几何?”其意思为:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈,上棱长2丈,高2丈,问:它的体积是多少?”已知l丈为10尺,该楔体的三视图如图所示,其中网格纸上小正方形边长为1,则该楔体的体积为( )

A. 10000立方尺 B. 11000立方尺
C. 12000立方尺 D. 13000立方尺
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数![]() ,
,![]() ,对于定义在
,对于定义在![]() 上的函数
上的函数![]() ,有下述命题:
,有下述命题:
①“![]() 是奇函数”的充要条件是“函数
是奇函数”的充要条件是“函数![]() 的图像关于点
的图像关于点![]() 对称”;
对称”;
②“![]() 是偶函数”的充要条件是“函数
是偶函数”的充要条件是“函数![]() 的图像关于直线
的图像关于直线![]() 对称”;
对称”;
③“![]() 是
是![]() 的一个周期”的充要条件是“对任意的
的一个周期”的充要条件是“对任意的![]() ,都有
,都有![]() ”;
”;
④“函数![]() 与
与![]() 的图像关于
的图像关于![]() 轴对称”的充要条件是“
轴对称”的充要条件是“![]() ”
”
其中正确命题的序号是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
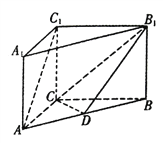
【题目】直三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() 上的动点.
上的动点.
(1)当点![]() 是
是![]() 的中点时,求证:
的中点时,求证: ![]() 平面
平面![]() ;
;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ?若存在,试求出
?若存在,试求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com