
【题目】已知函数![]() .
.
(Ⅰ)若![]() 的值域为
的值域为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在这祥的实数
,是否存在这祥的实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 内有且只有一个零点.若存在,求出
内有且只有一个零点.若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)存在,
;(Ⅱ)存在,![]()
【解析】
(1)![]() 的值域为
的值域为![]() ,则函数
,则函数![]() 必须是开口向上、与
必须是开口向上、与![]() 轴有唯一交点的二次函数.可以求出
轴有唯一交点的二次函数.可以求出![]() 的值.
的值.
(2)已知某函数零点个数,求参数问题,函数零点问题可以转化为方程根或者通过转化变成两图象交点个数问题.本题中令 ![]() ,则它的图象非常熟悉,而
,则它的图象非常熟悉,而![]() 在
在![]() ∈
∈![]() 的图象则需要考虑是否是二次函数,当确定是二次函数时,考虑函数的开口方向,对称轴与区间的位置关系(为了更好的研究函数在区间的单调性,便于考虑它的性质).
的图象则需要考虑是否是二次函数,当确定是二次函数时,考虑函数的开口方向,对称轴与区间的位置关系(为了更好的研究函数在区间的单调性,便于考虑它的性质).
(Ⅰ)函数![]() 的值域为
的值域为![]() ,则
,则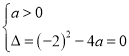 ,解得
,解得![]() .
.
(Ⅱ)由![]() ,
,
即![]()
令![]() ,
,![]() ,
,![]() ∈
∈![]() ,原命题等价于两个函数
,原命题等价于两个函数![]() 与
与![]() 的图象在
的图象在![]() 内有唯一交点.
内有唯一交点.
(1)当![]() 时,
时,![]() 在
在![]() 上递减,
上递减,![]() 在
在![]() 上递增,
上递增,
而g(1)=1>0=h(1),g(2)=-1<1=h(2),
∴函数![]() 与
与![]() 的图象在
的图象在![]() 内有唯一交点.
内有唯一交点.
(2)当![]() 时,
时,![]() 图象开口向下,对称轴为
图象开口向下,对称轴为![]() ,
,![]() 在
在![]() 上递减,
上递减,
![]() 在
在![]() 上递增,
上递增,![]() 与
与![]() 的图象在
的图象在![]() 内有唯一交点,
内有唯一交点,
当且仅当![]() ,即
,即![]() 即
即![]() .
.
∴![]()
(3)当![]() 时,
时,![]() 图象开口向上,对称轴为
图象开口向上,对称轴为![]() ,
,![]() 在
在![]() 上递减,
上递减,![]() 在
在![]() 上递增,
上递增,![]() 与
与![]() 的图象在
的图象在![]() 内有唯一交点,
内有唯一交点,
![]() ,即
,即![]() 即
即![]() ,
,
∴![]() .
.
综上,存在实数![]() ,使函数
,使函数![]() 于在区间
于在区间![]() 内有且只有一个点.
内有且只有一个点.


科目:高中数学 来源: 题型:
【题目】已知过原点![]() 的动直线
的动直线![]() 与圆
与圆![]() :
: ![]() 交于
交于![]() 两点.
两点.
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得当
,使得当![]() 变动时,总有直线
变动时,总有直线![]() 的斜率之和为0?若存在,求出
的斜率之和为0?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且△PF1F2的面积为2.
,且△PF1F2的面积为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为1的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于A,B两点,与椭圆C交于C,D两点,且
的圆交于A,B两点,与椭圆C交于C,D两点,且![]() (
(![]() ),当
),当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)设![]() ,当
,当![]() 时,
时,![]() 的值域为
的值域为![]() ,试求
,试求![]() 与
与![]() 的值;
的值;
(3)当![]() 时,记
时,记![]() ,如果对于区间
,如果对于区间![]() 上的任意三个实数
上的任意三个实数![]() 、
、![]() 、
、![]() ,都存在以
,都存在以![]() 、
、![]() 、
、![]() 为边长的三角形,求实数
为边长的三角形,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)设![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)设![]() 且
且![]() 时,
时,![]() 的定义域和值域都是
的定义域和值域都是![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
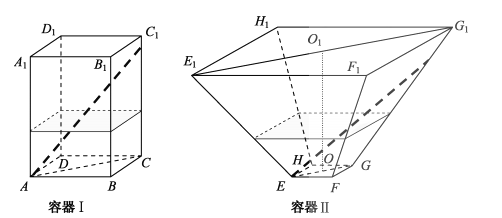
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com