
若 ,其中
,其中 .
.
(1)当 时,求函数
时,求函数 在区间
在区间 上的最大值;
上的最大值;
(2)当 时,若
时,若 恒成立,求
恒成立,求 的取值范围.
的取值范围.
(1)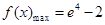 ;(2)
;(2)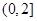 .
.
解析试题分析:本题主要考查导数的运算,利用导数研究函数的单调性,最值和不等式等基础知识,考查函数思想,分类讨论思想,考查综合分析和解决问题的能力.第一问,当 时,函数解析式确定,并不是分段函数,这就降低了试题的难度,求导数,判断所求区间上函数的单调性,再求最值,第一问较简单;第二问,由于函数
时,函数解析式确定,并不是分段函数,这就降低了试题的难度,求导数,判断所求区间上函数的单调性,再求最值,第一问较简单;第二问,由于函数 是分段函数,所以根据函数定义域把所求区间从
是分段函数,所以根据函数定义域把所求区间从 断开,充分考查了分类讨论思想,求出每段范围内函数的最小值来解决恒成立问题.
断开,充分考查了分类讨论思想,求出每段范围内函数的最小值来解决恒成立问题.
试题解析:(1)当 ,
,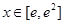 时,
时, ,
,
∵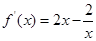 ,∴当
,∴当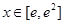 时,
时, 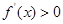 ,
,
∴函数 在
在 上单调递增,
上单调递增,
故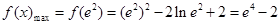 .(4分)
.(4分)
(2)①当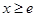 时,
时,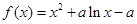 ,
,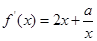 ,
,
∵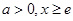 ,∴
,∴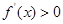 ,∴
,∴ 在
在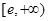 上为增函数,
上为增函数,
故当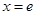 时,
时,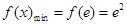 ;
;
②当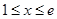 时,
时,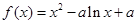 ,
,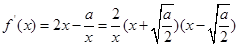 ,
,
(ⅰ)当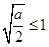 即
即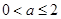 时,
时, 在区间
在区间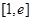 上为增函数,
上为增函数,
当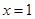 时,
时,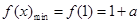 ,且此时
,且此时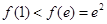 ;
;
(ⅱ)当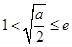 ,即
,即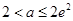 时,
时, 在区间
在区间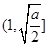 上为减函数,在区间
上为减函数,在区间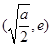 上为增函数,
上为增函数,
故当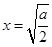 时,
时,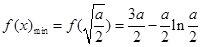 ,且此时
,且此时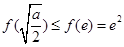 ;
;
(ⅲ)当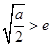 ,即
,即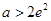 时,
时,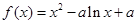 在区间
在区间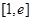 上为减函数,
上为减函数,
故当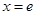 时,
时,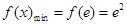 .
.
综上所述,函数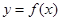 在
在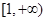 上的最小值为
上的最小值为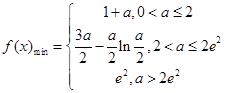
由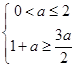 ,得
,得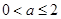 ;由
;由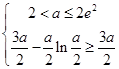 ,得无解;
,得无解;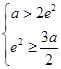 ,得无解;
,得无解;
故所求 的取值范围是
的取值范围是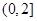 .(12分)
.(12分)
考点:1.用导数求函数最值;2.恒成立问题;3.用导数判断函数的单调性.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:高中数学 来源: 题型:解答题
(理)已知函数f(x)=  -lnx,x∈[1,3].
-lnx,x∈[1,3].
(Ⅰ)求f(x)的最大值与最小值;
(Ⅱ)若f(x)<4-At对于任意的x∈[1,3],t∈[0,2]恒成立,求实数A的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义在 上的函数
上的函数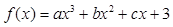 同时满足以下条件:①函数
同时满足以下条件:①函数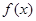 在
在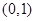 上是减函数,在
上是减函数,在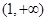 上是增函数;②
上是增函数;②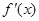 是偶函数;③函数
是偶函数;③函数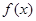 在
在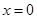 处的切线与直线
处的切线与直线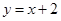 垂直.
垂直.
(Ⅰ)求函数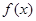 的解析式;
的解析式;
(Ⅱ)设 ,若存在
,若存在 使得
使得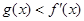 ,求实数
,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)= +aln(x-1)(a∈R).
+aln(x-1)(a∈R).
(Ⅰ)若f(x)在[2,+∞)上是增函数,求实数a的取值范围;
(Ⅱ)当a=2时,求证:1- <2ln(x-1)<2x-4(x>2);
<2ln(x-1)<2x-4(x>2);
(Ⅲ)求证: +
+ +…+
+…+ <lnn<1+
<lnn<1+ + +
+ + (n∈N*,且n≥2).
(n∈N*,且n≥2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com