
【题目】已知数列{an}的前n项和Sn=﹣an﹣( ![]() )n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
)n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
(Ⅰ)求证数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)设cn=log2 ![]() ,数列{
,数列{ ![]() }的前n项和为Tn , 求满足Tn
}的前n项和为Tn , 求满足Tn ![]() (n∈N*)的n的最大值.
(n∈N*)的n的最大值.
【答案】(Ⅰ)证明:∵Sn=﹣an﹣( ![]() )n﹣1+2(n∈N+),当n≥2时,Sn﹣1=﹣an﹣1﹣(
)n﹣1+2(n∈N+),当n≥2时,Sn﹣1=﹣an﹣1﹣( ![]() )n﹣2+2(n∈N+),
)n﹣2+2(n∈N+),
∴an=Sn﹣Sn﹣1=﹣an+an﹣1+( ![]() )n﹣1 ,
)n﹣1 ,
化为2nan=2n﹣1an﹣1+1.
∵bn=2nan . ∴bn=bn﹣1+1,即当n≥2时,bn﹣bn﹣1=1.
令n=1,可得S1=﹣a1﹣1+2=a1 , 即a1= ![]() .
.
又b1=2a1=1,∴数列{bn}是首项和公差均为1的等差数列.
于是bn=1+(n﹣1)1=n=2nan ,
∴an= ![]() .
.
(Ⅱ)解:∵cn=log2![]() =n,
=n,
∴ ![]() =
= ![]() ﹣
﹣ ![]() ,
,
∴Tn=(1﹣ ![]() )+(
)+( ![]() ﹣
﹣ ![]() )+…(
)+…( ![]() ﹣
﹣ ![]() )=1+
)=1+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ,
,
由Tn![]() ,得1+
,得1+ ![]() ﹣
﹣ ![]() ﹣
﹣ ![]() ,即
,即 ![]() +
+ ![]() >
> ![]() ,
,
∵f(n)= ![]() +
+ ![]() 单调递减,f(4)=
单调递减,f(4)= ![]() ,f(5)=
,f(5)= ![]() ,
,
∴n的最大值为4.
【解析】(Ⅰ)利用“当n≥2时,an=Sn﹣Sn﹣1”及其等差数列的通项公式即可得出.(Ⅱ)先求通项,再利用裂项法求和,进而解不等式,即可求得正整数n的最大值.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】定义函数F(a,b)= ![]() (a+b﹣|a﹣b|)(a,b∈R),设函数f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函数F(f(x),g(x))的最大值与零点之和为( )
(a+b﹣|a﹣b|)(a,b∈R),设函数f(x)=﹣x2+2x+4,g(x)=x+2(x∈R)函数F(f(x),g(x))的最大值与零点之和为( )
A.4
B.6
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的短轴长为2,离心率e=
=1(a>b>0)的短轴长为2,离心率e= ![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=kx+m与椭圆交于不同的两点A,B,与圆x2+y2= ![]() 相切于点M.
相切于点M.
(i)证明:OA⊥OB(O为坐标原点);
(ii)设λ= ![]() ,求实数λ的取值范围.
,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N* , 总有b1b2b3…bn﹣1bn=an+2成立.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记cn=(﹣1)n ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,⊙O是以AB为直径的圆,点C在圆上,在△ABC和△ACD中,∠ADC=90°,∠BAC=∠CAD,DC的延长线与AB的延长线交于点E.若EB=6,EC=6 ![]() ,则BC的长为 .
,则BC的长为 . 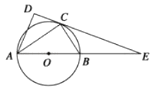
查看答案和解析>>
科目:高中数学 来源: 题型:
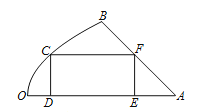
【题目】如图是一块地皮![]() ,其中
,其中![]() ,
, ![]() 是直线段,曲线段
是直线段,曲线段![]() 是抛物线的一部分,且点
是抛物线的一部分,且点![]() 是该抛物线的顶点,
是该抛物线的顶点, ![]() 所在的直线是该抛物线的对称轴.经测量,
所在的直线是该抛物线的对称轴.经测量, ![]() km,
km, ![]() km,
km, ![]() .现要从这块地皮中划一个矩形
.现要从这块地皮中划一个矩形![]() 来建造草坪,其中点
来建造草坪,其中点![]() 在曲线段
在曲线段![]() 上,点
上,点![]() ,
, ![]() 在直线段
在直线段![]() 上,点
上,点![]() 在直线段
在直线段![]() 上,设
上,设![]() km,矩形草坪
km,矩形草坪![]() 的面积为
的面积为![]() km2.
km2.
(1)求![]() ,并写出定义域;
,并写出定义域;
(2)当![]() 为多少时,矩形草坪
为多少时,矩形草坪![]() 的面积最大?
的面积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有4个人去参加某娱乐活动,该活动有甲、乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏.
(Ⅰ)求这4个人中恰有2人去参加甲游戏的概率;
(Ⅱ)用X,Y分别表示这4个人中去参加甲、乙游戏的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列与数学期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学城校区与本部校区之间的驾车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
| 25 | 30 | 35 | 40 |
频数(次) | 100 | 150 | 200 | 50 |
以这500次驾车单程所需时间的频率代替某人1次驾车单程所需时间的概率.
(1)求![]() 的分布列与
的分布列与![]() ;
;
(2)某天有3位教师独自驾车从大学城校区返回本部校区,记![]() 表示这3位教师中驾车所用时间少于
表示这3位教师中驾车所用时间少于![]() 的人数,求
的人数,求![]() 的分布列与
的分布列与![]() ;
;
(3)下周某天张老师将驾车从大学城校区出发,前往本部校区做一个50分钟的讲座,结束后立即返回大学城校区,求张老师从离开大学城校区到返回大学城校区共用时间不超过120分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若ξ服从正态分布N(0,2),且P(ξ>2)=0.4,则P(0<ξ<2)=0.2
B.x=1是x2﹣x=0的必要不充分条件
C.直线ax+y+2=0与ax﹣y+4=0垂直的充要条件为a=±1
D.“若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0”
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com