练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    E，F分别为正方形ABCD的AB与CD的中点，把正方形沿EF折起，使平面AEFD⊥平面EBCF，则cos∠EDB∶cos∠DBC＝________．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    如图是一几何体的平面展开图，其中四边形ABCD为正方形，E、F分别为PA、PD的中点，在此几何体中，给出下面四个结论：①直线BE与直线CF是异面直线；②直线BE与直线AF是异面直线；③直线EF∥平面PBC；④平面BCE⊥平面PAD．其中正确结论的序号是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2011•蓝山县模拟）如图，在四棱锥P-ABCD中，底面ABCD是边长为a的正方形，E、F分别为PC、BD的中点，侧面PAD⊥底面ABCD，且PA=PD=
    		2
    2
    AD．
    （1）求证：EF∥平面PAD；
    （2）求证：PA⊥平面PCD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

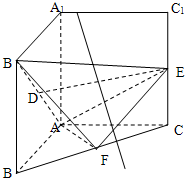    （2012•平遥县模拟）把正方形AA1B1B以边AA1所在直线为轴旋转900到正方形AA1C1C，其中D，E，F分别为B1A，C1C，BC的中点．
    （1）求证：DE∥平面ABC；
    （2）求证：B1F⊥平面AEF；
    （3）求二面角A-EB1-F的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图所示，过正方形ABCD的中心O作OP⊥平面ABCD，已知正方形的边长为2，OP=2，连接AP、BP、CP、DP，M、N分别是AB、BC的中点，以O为原点，射线OM、ON、OP分别为Ox轴、Oy轴、Oz轴的正方向建立空间直角坐标系．若E、F分别为PA、PB的中点，求A、B、C、D、E、F的坐标．

    查看答案和解析>>

    科目：高中数学 来源：名师指点学高中课程 数学 高二（下） 题型：013

    已知E、F分别为正方形ABCD的边AB、CD的中点，EF与BD交于O，以 EF为棱将正方形折成直二面角，则∠BOD等于

    [　　]

    A．
    B．
    C．
    D．

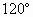
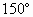
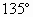
    查看答案和解析>>

    同步练习册答案