
如图,在四棱锥 中,底面
中,底面 为矩形,
为矩形, 平面
平面 ,
, ,
, 为
为 中点.
中点.

(1)证明: //平面
//平面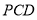 ;
;
(2)证明: 平面
平面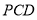 .
.
(1)参考解析;(2)参考解析
【解析】
试题分析:(1)直线与平面平行的证明,根据判断定理要在平面内找一条直线与与该直线平行.所以要证 //平面
//平面 ,找到直线
,找到直线 即可.
即可.
(2)要证直线与平面垂直根据判断定理要在平面内找到两条相交的直线与该直线垂直即可.通过分析直线AE⊥PD由题意可得;另外直线CD垂直平面PAD,所以有可得直线CD垂直直线AE.又由于直线CD与直线PD相交,所以可证得结论.
试题解析:证明:(1)因为底面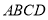 为矩形,
为矩形,
所以  .又因为
.又因为 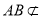 平面
平面 ,
, 平面
平面 ,
,
所以  //平面
//平面 .
.
(2)因为 ,
, 为
为 中点,
中点,

所以 ,因为
,因为  平面
平面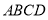 ,
,
所以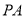
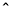
 .又底面
.又底面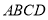 为矩形,
为矩形,
所以 .
.
所以 平面
平面 .
.
所以
 .
.
所以 平面
平面 .
.
考点:1.线面平行的判断.2.线面垂直的判断.3.线面关系与线线关系的相互转化.4.空间图像感.


科目:高中数学 来源:2015届北京市西城区高二第一学期期末文科数学试卷(解析版) 题型:解答题
已知抛物线 ,点
,点 ,过
,过 的直线
的直线 交抛物线
交抛物线 于
于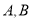 两点.
两点.
(1)若 ,抛物线
,抛物线 的焦点与
的焦点与 中点的连线垂直于
中点的连线垂直于 轴,求直线
轴,求直线 的方程;
的方程;
(2)设 为小于零的常数,点
为小于零的常数,点 关于
关于 轴的对称点为
轴的对称点为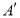 ,求证:直线
,求证:直线 过定点
过定点
查看答案和解析>>
科目:高中数学 来源:2015届北京市西城区高二第一学期期末文科数学试卷(解析版) 题型:选择题
关于直线 以及平面
以及平面 ,下列命题中正确的是 ( )
,下列命题中正确的是 ( )
A. 若 ,则
,则 B. 若
B. 若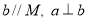 ,则
,则
C. 若 ,则
,则 D. 若
D. 若 ,则
,则
查看答案和解析>>
科目:高中数学 来源:2015届北京东城(南片)高二上学期期末考试理数学试卷(解析版) 题型:选择题
平面 平面
平面 的一个充分条件是
的一个充分条件是
A. 存在一条直线 ,
, 且
且
B. 存在一个平面 ,
, ∥
∥ 且
且 ∥
∥
C. 存在一个平面 ,
, ⊥
⊥ 且
且 ⊥
⊥
D. 存在一条直线 ,
, 且
且 ∥
∥
查看答案和解析>>
科目:高中数学 来源:2015届北京东城区高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
“ ”是“直线
”是“直线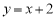 与圆
与圆 相切”的( )
相切”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com