
【题目】已知双曲线的中心在原点,焦点F1、F2在坐标轴上,焦距是实轴长的![]() 倍且过点(4,﹣
倍且过点(4,﹣![]() )
)
(1)求双曲线方程;
(2)若点M(3,m)在双曲线上,求证:点M在以F1F2为直径的圆上;
(3)在(2)条件下,若M F2交双曲线另一点N,求△F1MN的面积.
【答案】(1)x2﹣y2=6;(2)证明见解析;(3)![]()
【解析】
(1)求出离心率e,故可等轴设双曲线的方程为x2﹣y2=λ(λ≠2),过点(4,﹣![]() ),可得16﹣10=λ,即可求双曲线方程;
),可得16﹣10=λ,即可求双曲线方程;
(2)求出向量坐标,利用向量的数量积公式,即可证明结论.
(3)利用M与F2可得直线方程,求出N的纵坐标,然后求解三角形的面积.
(1)∵焦距是实轴长的![]() 倍,
倍,
∴e=![]() ,故可等轴设双曲线的方程为x2﹣y2=λ(λ≠2),
,故可等轴设双曲线的方程为x2﹣y2=λ(λ≠2),
∵过点(4,﹣![]() ),∴16﹣10=λ,
),∴16﹣10=λ,
∴λ=6.
∴双曲线方程为x2﹣y2=6.
(2)证明:由(1)可知:在双曲线中,a=b=![]() ,∴c=2
,∴c=2![]() .
.
∴F1(﹣2![]() ,0),F2(2
,0),F2(2![]() ,0).
,0).
∴![]() =(﹣2
=(﹣2![]() ﹣3,﹣m),
﹣3,﹣m),
![]() =(2
=(2![]() ﹣3,﹣m).
﹣3,﹣m).
∴![]() =+m2=﹣3+m2.
=+m2=﹣3+m2.
∵M点在双曲线上,∴9﹣m2=6,∴m2=3.
∴![]() ,
,
∴点M在以F1F2为直径的圆上;
(3)由(2)不妨M(3,![]() ),F2(2
),F2(2![]() ,0),直线M F2的方程为:y=(﹣2﹣
,0),直线M F2的方程为:y=(﹣2﹣![]() )(x﹣2
)(x﹣2![]() ),代入双曲线方程可得:
),代入双曲线方程可得:
消去x可得:(6﹣4![]() )y2﹣4
)y2﹣4![]() (2﹣
(2﹣![]() )y+6=0,
)y+6=0,
因为M的纵坐标为![]() ,
,
所以N的纵坐标为: ![]() ,
,
解得y2=﹣(2+![]() ),
),
△F1MN的面积为:![]() =12+4
=12+4![]() .
.


科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() 这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.
这两个条件中任选-一个,补充在下面问题中,然后解答补充完整的题.

在![]() 中,角
中,角![]() 的对边分别为
的对边分别为![]() ,已知 ,
,已知 ,![]() .
.
(1)求![]() ;
;
(2)如图,![]() 为边
为边![]() 上一点,
上一点,![]() ,求
,求![]() 的面积
的面积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构对全国互联网行业进行调查统计,得到整个互联网行业从业者年龄分布饼状图和90后从事互联网行业者岗位分布图(90后指1990年及以后出生,80后指1980-1989年之间出生,80前指1979年及以前出生),则下列结论中不一定正确的是( )
整个互联网行业从业者年龄分布饼状图 90后从事互联网行业者岗位分布图
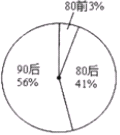
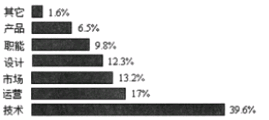
A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数90后比80后多
C.互联网行业中从事设计岗位的人数90后比80前多
D.互联网行业中从事市场岗位的90后人数不足总人数的10%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 是一个集合,
是一个集合,![]() 是一个以
是一个以![]() 的某些子集为元素的集合,且满足:(1)
的某些子集为元素的集合,且满足:(1)![]() 属于
属于![]() ,
,![]() 属于
属于![]() ;(2)
;(2)![]() 中任意多个元素的并集属于
中任意多个元素的并集属于![]() ;(3)
;(3)![]() 中任意多个元素的交集属于
中任意多个元素的交集属于![]() ,则称
,则称![]() 是集合
是集合![]() 上的一个拓补.已知集合
上的一个拓补.已知集合![]() ,对于下面给出的四个集合
,对于下面给出的四个集合![]() :
:
①![]() ②
②![]()
③![]() ④
④![]()
其中是集合![]() 上的拓补的集合
上的拓补的集合![]() 的序号是______.(写出所有的拓补的集合
的序号是______.(写出所有的拓补的集合![]() 的序号)
的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,离心率为
,离心率为![]() ,直线l经过
,直线l经过![]() 与椭圆交于P,Q两点.当
与椭圆交于P,Q两点.当![]() 与y轴的交点是线段
与y轴的交点是线段![]() 的中点时,
的中点时,![]() .
.
(1)求椭圆的方程;
(2)设直线l不垂直于x轴,若![]() 满足
满足![]() ,求t的取值范围.
,求t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com