
| A. | $\frac{24}{13}$ | B. | $-\frac{24}{13}$ | C. | $\frac{10}{13}$ | D. | $-\frac{10}{13}$ |
分析 利用同角三角函数关系式求出cos($\frac{π}{4}-x$),和与差的公式构造出cos2x,即可求出结果.
解答 解:∵0<x<$\frac{π}{4},sin(\frac{π}{4}-x)=\frac{5}{13}$,
∴$-\frac{π}{4}<\frac{π}{4}-x<\frac{π}{4}$,
∴cos($\frac{π}{4}-x$)=$\frac{12}{13}$.
cos2x═sin[($\frac{π}{4}-x$)$+(\frac{π}{4}-x)$]=2sin($\frac{π}{4}-x$)cos($\frac{π}{4}-x$)=2×$\frac{5}{13}×\frac{12}{13}$=$\frac{120}{169}$.
cos($\frac{π}{4}+x$)=sin($\frac{π}{2}-(\frac{π}{4}-x)$)=$\frac{5}{13}$,
那么:$\frac{cos2x}{{cos(\frac{π}{4}+x)}}$=$\frac{120}{169}×\frac{13}{5}=\frac{24}{13}$.
故选:A.
点评 本题主要考查了同角三角函数关系式和和与差公式的应用,属于基本知识的考查.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
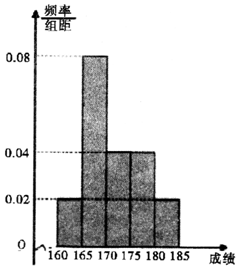 近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示:
近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设铁路AB长为100,BC⊥AB,且BC=30,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.
设铁路AB长为100,BC⊥AB,且BC=30,为将货物从A运往C,现在AB上距点B为x的点M处修一公路至C,已知单位距离的铁路运费为2,公路运费为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
| A. | 9400 | B. | 9408 | C. | 9410 | D. | 9414 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$或2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com