
【题目】设f(x)=asin 2x+bcos 2x,其中a,b∈R,ab≠0.若f(x)≤|f( ![]() )|对一切x∈R恒成立,则以下结论正确的是(写出所有正确结论的编号). ①
)|对一切x∈R恒成立,则以下结论正确的是(写出所有正确结论的编号). ① ![]() ;②
;② ![]() ≥
≥ ![]() ;
;
③f(x)的单调递增区间是(kπ+ ![]() ,kπ+
,kπ+ ![]() )(k∈Z);
)(k∈Z);
④f(x)既不是奇函数也不是偶函数.
【答案】①②④
【解析】解:由f(x)=asin 2x+bcos 2x= ![]() sin(2x+φ). ∵f(x)≤|f(
sin(2x+φ). ∵f(x)≤|f( ![]() )|对一切x∈R恒成立
)|对一切x∈R恒成立
∴当x= ![]() 时,函数取得最大值,即2×
时,函数取得最大值,即2× ![]() +φ=
+φ= ![]() ,解得:φ=
,解得:φ= ![]() .
.
故得f(x)= ![]() sin(2x+
sin(2x+ ![]() ).
).
则f( ![]() )=
)= ![]() sin(2×
sin(2× ![]() +
+ ![]() )=0,∴①对.
)=0,∴①对.
②f( ![]() )=
)= ![]() sin(2×
sin(2× ![]() +
+ ![]() )=-
)=- ![]()
f( ![]() )=
)= ![]() sin(2×
sin(2× ![]() +
+ ![]() )=
)= ![]() ,∴
,∴ ![]() ≥
≥ ![]() ,∴②对.
,∴②对.
由 ![]() 2x+
2x+ ![]() ,(k∈Z)
,(k∈Z)
解得:- ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,(k∈Z)
+kπ,(k∈Z)
∴f(x)的单调递增区间是(kπ- ![]() ,kπ+
,kπ+ ![]() )(k∈Z);∴③不对
)(k∈Z);∴③不对
f(x)的对称轴2x+ ![]() =
= ![]() +kπ,(k∈Z);∴③
+kπ,(k∈Z);∴③
解得:x= ![]() kπ+
kπ+ ![]() ,不是偶函数,
,不是偶函数,
当x=0时,f(0)= ![]() ,不关于(0,0)对称,
,不关于(0,0)对称,
∴f(x)既不是奇函数也不是偶函数.
所以答案是①②④.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】下列四个命题:
(1)随机误差e是衡量预报精确度的一个量,它满足E(e)=0
(2)残差平方和越小的模型,拟合的效果越好;
(3)用相关指数R2来刻画回归的效果时,R2的值越小,说明模型拟合的效果越好;
(4)直线y=bx+a和各点(x1 , y1),(x2 , y2),…,(xn , yn)的偏差 ![]() 是该坐标平面上所有直线与这些点的偏差中最小的直线.
是该坐标平面上所有直线与这些点的偏差中最小的直线.
其中真命题的个数( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)=ax2﹣(a+1)x+1
(1)解关于x的不等式f(x)>0;
(2)若对任意的a∈[﹣1,1],不等式f(x)>0恒成立,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=2,前n项和为Sn , 若Sn=2(an﹣1),(n∈N+).
(1)求数列{an}的通项公式;
(2)设bn=(log2an+1)2﹣(log2an)2 , 若cn=anbn , 求{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两名选手参加歌手大赛时,5名评委打的分数用茎叶图表示(如图).s1、s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是( ) 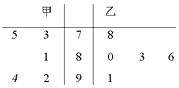
A.s1>s2
B.s1=s2
C.s1<s2
D.不确定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD为平行四边形,AB=3,AC=4,AD=5,SA⊥平面ABCD. 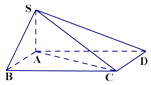
(1)证明:AC⊥平面SAB;
(2)若SA=2,求三棱锥A﹣SCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数 ![]() 在区间[﹣
在区间[﹣ ![]() ,
, ![]() ]上的图象时,列表并填入了部分数据,如表:
]上的图象时,列表并填入了部分数据,如表:
2x﹣ | ﹣ | ﹣π | ﹣ | 0 |
|
|
x | ﹣ | ﹣ | ﹣ |
|
|
|
f(x) |
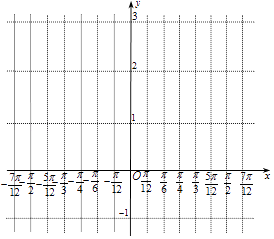
(1)请将上表数据补充完整,并在给出的直角坐标系中,画出f(x)在区间[﹣ ![]() ,
, ![]() ]上的图象;
]上的图象;
(2)求f(x)的最小值及取最小值时x的集合;
(3)求f(x)在 ![]() 时的值域.
时的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com