
【题目】已知等比数列![]() 满足:
满足:![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在正整数![]() ,使得
,使得![]() ?若存在,求
?若存在,求![]() 的最小值;若不存在,说明理由.
的最小值;若不存在,说明理由.
【答案】(1)an=![]() ·3n-1,或an=-5·(-1)n-1.
·3n-1,或an=-5·(-1)n-1.
(2)不存在正整数m,使得![]() ≥1成立.
≥1成立.
【解析】
试题(1)将已知条件转化为等比数列的首项和公比表示,转化为关于![]() 的方程组,通过解方程组得到
的方程组,通过解方程组得到![]() 的值,从而得到数列的通项公式;(2)将数列
的值,从而得到数列的通项公式;(2)将数列![]() 的通项公式代入
的通项公式代入![]() 求和,分情况判断对应的不等式是否成立
求和,分情况判断对应的不等式是否成立
试题解析:(1)设等比数列{an}的公比为q,
则由已知可得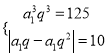
解得![]() 或
或![]()
故an=![]() ·3n-1,或an=-5·(-1)n-1.
·3n-1,或an=-5·(-1)n-1.
(2)若an=![]() ·3n-1,则
·3n-1,则![]() =
=![]() ·(
·(![]() )n-1.
)n-1.
故{![]() }是首项为
}是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
从而 .
.
若an=-5·(-1)n-1,则![]() =-
=-![]() (-1)n-1.
(-1)n-1.
故{![]() }是首项为-
}是首项为-![]() ,公比为-1的等比数列.
,公比为-1的等比数列.
从而![]() =
=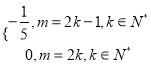 故
故![]() <1.
<1.
综上,对任何正整数m,总有![]() <1.
<1.
故不存在正整数m,使得![]() ≥1成立.
≥1成立.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 有且仅有三个公共点,求
有且仅有三个公共点,求![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上的三点![]() 、
、![]() 、
、![]() .
.
(1)求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的椭圆的标准方程;
的椭圆的标准方程;
(2)设点![]() 、
、![]() 、
、![]() 关于直线
关于直线![]() 的对称点分别为
的对称点分别为![]() 、
、![]() 、
、![]() ,求以
,求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的双曲线的标准方程.
的双曲线的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
已知中心在原点,顶点A1、A2在x轴上,其渐近线方程是![]() ,双曲线过点
,双曲线过点![]()
(1)求双曲线方程
(2)动直线![]() 经过
经过![]() 的重心G,与双曲线交于不同的两点M、N,问:是否存在直线
的重心G,与双曲线交于不同的两点M、N,问:是否存在直线![]() ,使G平分线段MN,证明你的结论
,使G平分线段MN,证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为征求个人所得税法修改建议,某机构对当地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1000,1500)).
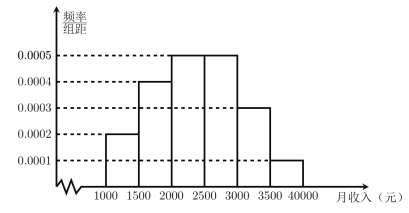
(1)求居民月收入在![]() 的频率;
的频率;
(2)根据频率分布直方图估算样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中用分层抽样方法抽出100人作进一步分析,则月收入在![]() 的这段应抽多少人?
的这段应抽多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com