
已知双曲线C的方程为 -
- =1(a>0,b>0),离心率e=
=1(a>0,b>0),离心率e= ,顶点到渐近线的距离为
,顶点到渐近线的距离为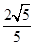 .
.
(1)求双曲线C的方程;
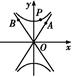
(2)如图,P是双曲线C上一点,A、B两点在双曲线C的两条渐近线上,且分别位于第一、二象限.若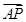 =λ
=λ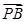 ,λ∈
,λ∈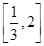 .求△AOB的面积的取值范围.
.求△AOB的面积的取值范围.
(1)  -x2=1 (2)
-x2=1 (2) 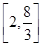
解析解:(1)由题意知,双曲线C的顶点(0,a)到渐近线ax-by=0的距离为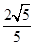 ,
,
∴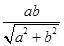 =
=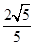 ,即
,即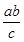 =
=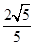 .
.
由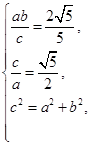 得
得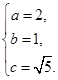
∴双曲线C的方程为 -x2=1.
-x2=1.
(2)由(1)知双曲线C的两条渐近线方程为y=±2x,
设A(m,2m),B(-n,2n),m>0,n>0.
由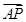 =λ
=λ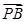 得P点坐标为
得P点坐标为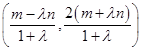 ,
,
将P点坐标代入 -x2=1,化简得mn=
-x2=1,化简得mn=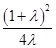 .
.
设∠AOB=2θ,∵tan(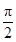 -θ)2.
-θ)2.
∴tanθ= ,sin2θ=
,sin2θ=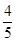 .
.
又|OA|= m,|OB|=
m,|OB|= n,
n,
∴S△AOB= |OA|·|OB|·sin2θ
|OA|·|OB|·sin2θ
=2mn
=
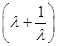 +1,
+1,
记S(λ)=
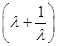 +1,λ∈
+1,λ∈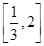 .
.
则S′(λ)=
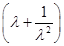 .
.
由S′(λ)=0得λ=1.
又S(1)=2,S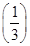 =
=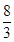 ,S(2)=
,S(2)=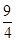 ,
,
∴当λ=1时,△AOB的面积取得最小值2,当λ= 时,
时,
△AOB的面积取得最大值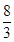 .
.
∴△AOB面积的取值范围是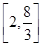 .
.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:解答题
设A、B分别为椭圆 =1(a>b>0)的左、右顶点,椭圆长半轴的长等于焦距,且直线x=4是它的右准线.
=1(a>b>0)的左、右顶点,椭圆长半轴的长等于焦距,且直线x=4是它的右准线.
(1)求椭圆的方程;
(2)设P为椭圆右准线上不同于点(4,0)的任意一点,若直线BP与椭圆相交于两点B、N,求证:∠NAP为锐角.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知A,B分别是椭圆C1: +
+ =1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2:
=1的左、右顶点,P是椭圆上异于A,B的任意一点,Q是双曲线C2: -
- =1上异于A,B的任意一点,a>b>0.
=1上异于A,B的任意一点,a>b>0.
(1)若P( ,
, ),Q(
),Q(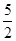 ,1),求椭圆C1的方程;
,1),求椭圆C1的方程;
(2)记直线AP,BP,AQ,BQ的斜率分别是k1,k2,k3,k4,求证:k1·k2+k3·k4为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为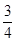 .
.
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由.
(3)若点M的横坐标为 ,直线l:y=kx+
,直线l:y=kx+ 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当 ≤k≤2时,|AB|2+|DE|2的最小值.
≤k≤2时,|AB|2+|DE|2的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知椭圆C: +
+ =1(a>b>0)的一个顶点为A(2,0),离心率为
=1(a>b>0)的一个顶点为A(2,0),离心率为 .直线y=k(x-1)与椭圆C交于不同的两点M,N.
.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为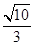 时,求k的值.
时,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知常数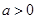 ,向量
,向量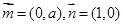 ,经过定点
,经过定点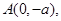 以
以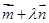 为方向向量的直线与经过定点
为方向向量的直线与经过定点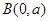 以
以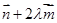 为方向向量的直线相交于
为方向向量的直线相交于 ,其中
,其中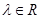 ,
,
(1)求点 的轨迹
的轨迹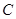 的方程;(2)若
的方程;(2)若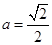 ,过
,过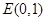 的直线交曲线
的直线交曲线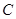 于
于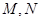 两点,求
两点,求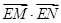 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我校某同学设计了一个如图所示的“蝴蝶形图案(阴影区域)”来庆祝数学学科节的成功举办.其中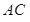 、
、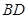 是过抛物线
是过抛物线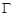 焦点
焦点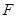 的两条弦,且其焦点
的两条弦,且其焦点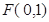 ,
,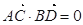 ,点
,点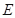 为
为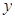 轴上一点,记
轴上一点,记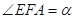 ,其中
,其中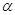 为锐角.
为锐角.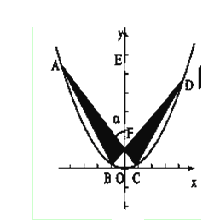
(1)求抛物线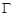 方程;
方程;
(2)当“蝴蝶形图案”的面积最小时求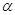 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com