
【题目】已知椭圆的中心在原点,焦点在x轴上![]() 分别为左、右焦点,椭圆的一个顶点与两焦点构成等边三角形,且
分别为左、右焦点,椭圆的一个顶点与两焦点构成等边三角形,且![]() .
.
(1)求椭圆方程;
(2)对于x轴上的某一点T,过T作不与坐标轴平行的直线L交椭圆于![]() 两点,若存在x轴上的点S,使得对符合条件的L恒有
两点,若存在x轴上的点S,使得对符合条件的L恒有![]() 成立,我们称S为T的一个配对点,当T为左焦点时,求T的配对点的坐标;
成立,我们称S为T的一个配对点,当T为左焦点时,求T的配对点的坐标;
(3)在(2)条件下讨论当T在何处时,存在有配对点?
【答案】(1)![]() (2)(-4,0)(3)
(2)(-4,0)(3)![]()
【解析】
(1)设椭圆的顶点为P,由![]() 可得
可得![]() ,由
,由![]() 结合椭圆的定义可得2a,结合
结合椭圆的定义可得2a,结合![]() 可求椭圆的方程
可求椭圆的方程
(2)可设过T的直线方程为![]() ,
,![]() ,联立椭圆方程整理可得
,联立椭圆方程整理可得![]() ,设
,设![]() ,
,![]() ,
,![]() ,由
,由![]() 得
得![]() 即
即![]() ,结合方程的根与系数的关系代入可求a
,结合方程的根与系数的关系代入可求a
(3)设![]() ,直线
,直线![]() 的方程
的方程![]() ,
,![]() ,使得对符合条件的L恒有
,使得对符合条件的L恒有![]() 成立,则T必须在
成立,则T必须在![]() 之间即
之间即![]()
同(2)的整理方法,联立直线与椭圆方程由![]() 可得,
可得,![]() ,同(2)的方法一样代入可求
,同(2)的方法一样代入可求
解:(1)设椭圆的顶点为P,由![]() 可得
可得![]()
![]() 可得
可得![]()
![]() ,
,![]()
椭圆的方程为:![]()
(2)![]() ,
,
则过可设过T的直线方程为![]() ,
,![]() ,
,
联立椭圆方程整理可得![]()
设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]()
![]()
![]()
![]()
整理可得![]()
即![]()
![]()
(3)设![]() ,直线
,直线![]() 的方程
的方程![]() ,
,![]()
使得对符合条件的L恒有![]() 成立,则T必须在
成立,则T必须在![]() 之间即
之间即![]()
同(2)的整理方法,联立直线与椭圆方程可得,![]() ,
,![]()
由![]() 可得,
可得,![]()
同(2)的方法一样代入可求![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足:
满足:![]() ,
,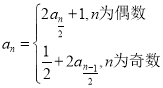 ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)设![]() ,求证:数列
,求证:数列![]() 是等比数列,并求出其通项公式;
是等比数列,并求出其通项公式;
(3)对任意的![]() ,
,![]() ,在数列
,在数列![]() 中是否存在连续的
中是否存在连续的![]() 项构成等差数列?若存在,写出这
项构成等差数列?若存在,写出这![]() 项,并证明这
项,并证明这![]() 项构成等差数列:若不存在,请说明理由.
项构成等差数列:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() (
(![]() ).
).
(1)计算![]() ,
,![]() ,
,![]() ,
,![]() ,并求数列
,并求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足
满足![]() ,求证:数列
,求证:数列![]() 是等比数列;
是等比数列;
(3)由数列![]() 的项组成一个新数列
的项组成一个新数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,设
,设![]() 为数列
为数列![]() 的前
的前![]() 项和,试求
项和,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
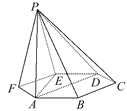
【题目】如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.
其中正确的有____________(把所有正确的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,若
,若![]() ,则称
,则称![]() 是“
是“![]() 数列”.
数列”.
(1)若![]() 是“
是“![]() 数列”,且
数列”,且![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若![]() 是等差数列,首项为
是等差数列,首项为![]() ,公差为
,公差为![]() ,且
,且![]() ,判断
,判断![]() 是否为“
是否为“![]() 数列”;
数列”;
(3)设数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,若数列
,若数列![]() 与
与![]() 都是“
都是“![]() 数列”,求
数列”,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】符合以下性质的函数称为“![]() 函数”:①定义域为
函数”:①定义域为![]() ,②
,②![]() 是奇函数,③
是奇函数,③![]() (常数
(常数![]() ),④
),④![]() 在
在![]() 上单调递增,⑤对任意一个小于
上单调递增,⑤对任意一个小于![]() 的正数
的正数![]() ,至少存在一个自变量
,至少存在一个自变量![]() ,使
,使![]() .下列四个函数中
.下列四个函数中![]() ,
,![]() ,
, ,
, 中“
中“![]() 函数”的个数为( )
函数”的个数为( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为实数),
为实数),![]() .
.
(1)若函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的解析式;
的解析式;
(2)在(1)的条件下,![]() 在区间
在区间![]() 上恒成立,试求
上恒成立,试求![]() 的取值范围;
的取值范围;
(3)若![]() ,
,![]() 为偶函数,实数
为偶函数,实数![]() ,
,![]() 满足
满足![]() ,
,![]() ,定义函数
,定义函数 ,试判断
,试判断![]() 值的正负,并说明理由.
值的正负,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当前,旅游已经成为新时期人民群众美好生活和精神文化需求的重要内容.旅游是综合性产业,是拉动经济发展的重要动力,也为整个经济结构调整注入活力.文化旅游产业研究院发布了《2019年中国文旅产业发展趋势报告》,报告指出:旅游业稳步增长,每年占国家GDP总量的比例逐年增加,如图及下表为2014年到2018年的相关统计数据.
旅游收入占国家GDP总量比例趋势 | |||||
年份: | 1 | 2 | 3 | 4 | 5 |
占比: | 10.4 | 10.8 | 11.0 | 11.0 | 11.2 |
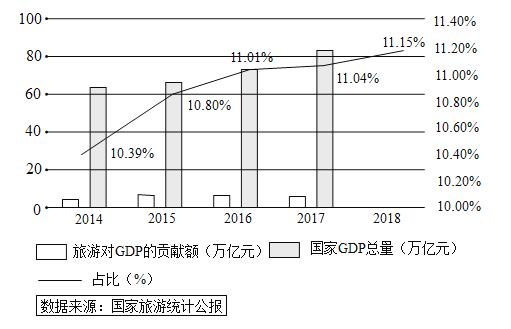
(1)根据以上数据,求出占比![]() 关于年份
关于年份![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据(1)所求线性回归方程,预测2019年的旅游收入所占的比例.
附: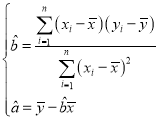 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]()
![]() 的离心率为
的离心率为![]() ,右准线的方程为
,右准线的方程为![]()
![]()
![]() 分别为椭圆C的左、右焦点,A,B分别为椭圆C的左、右顶点.
分别为椭圆C的左、右焦点,A,B分别为椭圆C的左、右顶点.
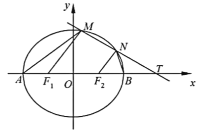
(1)求椭圆C的标准方程;
(2)过![]()
![]() 作斜率为
作斜率为![]()
![]() 的直线l交椭圆C于M,N两点(点M在点N的左侧),且
的直线l交椭圆C于M,N两点(点M在点N的左侧),且![]() ,设直线AM,BN的斜率分别为
,设直线AM,BN的斜率分别为![]()
![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com