
(本题满分12分,每一问6分)
如图,弧 是半径为
是半径为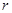 的半圆,
的半圆,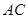 为直径,点
为直径,点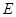 为弧
为弧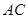 的中点,点
的中点,点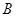 和点
和点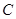 为线段
为线段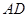 的三等分点,线段
的三等分点,线段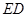 与弧
与弧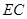 交于点
交于点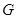 ,且
,且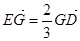 ,平面
,平面 外一点
外一点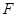 满足
满足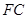
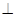 平面
平面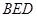 ,
,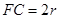 。
。

⑴证明:
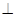
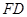 ;
;
⑵ 将 (及其内部)绕
(及其内部)绕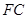 所在直线旋转一周形成一几何体,求该几何体的体积。
所在直线旋转一周形成一几何体,求该几何体的体积。
⑴ 证明: 见解析;⑵ 。
。
【解析】本试题主要是考查了圆内几何性质,以及线面垂直的判定定理,以及关于圆锥的体积的运算的综合运用。
(1)由于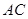 为直径,点
为直径,点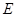 为弧
为弧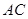 的中点,
的中点,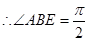 ,即
,即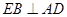 又
又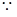
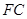
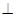 平面
平面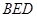 ,
,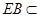 平面
平面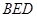 ,
,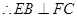 ,进而得到线面垂直,利用性质定理得到线线垂直的证明。
,进而得到线面垂直,利用性质定理得到线线垂直的证明。
(2)建立空间直角坐标系,则相关点的坐标为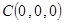 ,
,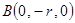 ,
,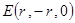 ,
,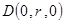 ,利用两点的距离公式得到高的长度,然后求解椎体的体积公式即可。
,利用两点的距离公式得到高的长度,然后求解椎体的体积公式即可。
⑴ 证明: 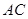 为直径,点
为直径,点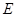 为弧
为弧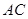 的中点,
的中点,
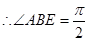 ,即
,即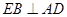 。………2分
。………2分
又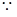
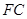
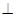 平面
平面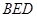 ,
,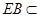 平面
平面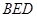 ,
,
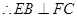 ,
,
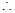 由
由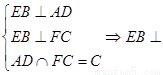 平面
平面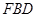 ,……4分
,……4分
又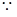
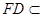 平面
平面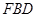 ,
,
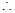
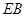
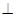
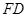 。…………………………………………………………………………6分
。…………………………………………………………………………6分
⑵ 如图所示,建立空间直角坐标系,则相关点的坐标为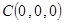 ,
,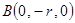 ,
,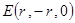 ,
,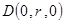 ,……………………………………7分
,……………………………………7分
设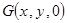 则由
则由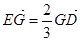 ,得
,得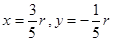
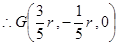 ,……………………………………………………………………9分
,……………………………………………………………………9分
则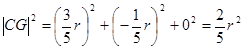 ,由题设知,所得几何体为圆锥,其底面积为
,由题设知,所得几何体为圆锥,其底面积为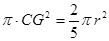 ,高为
,高为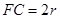 。…………………………………………………11分
。…………………………………………………11分
所以该圆锥的体积为 。………………………………12分
。………………………………12分


科目:高中数学 来源:2012-2013学年福建省高三第一次阶段考试文科数学试卷(解析版) 题型:解答题
(本题满分12分,每小题6分)
(1)若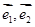 为基底向量,且
为基底向量,且 若A、B、D三点共线,求实数k的值;
若A、B、D三点共线,求实数k的值;
(2)用“五点作图法”在已给坐标系中画出函数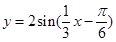 一个周期内的简图,并指出该函数图象是由函数
一个周期内的简图,并指出该函数图象是由函数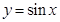 的图象进行怎样的变换而得到的?
的图象进行怎样的变换而得到的?
查看答案和解析>>
科目:高中数学 来源:2011-2012学年上海市高三第一学期期中考试试题数学 题型:解答题
本题满分12分,每小题各4分)
已知函数 ,
,
(1)若函数 的值域为
的值域为 ,求实数a的值;
,求实数a的值;
(2)若函数 的递增区间为
的递增区间为 ,求实数a的值;
,求实数a的值;
(3)若函数 在区间
在区间 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:福建省09-10学年高二第二学期期末考试数学试题文科 题型:解答题
(本题满分12分)
我市旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售a(a>0)件. 通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为x (0<x<1),那么月平均销售量减少的百分率为x2.记改进工艺后,旅游部门销售该纪念品的月平均利润是y(元)
(Ⅰ)写出y与x的函数关系式;
(Ⅱ)改进工艺后,确定该纪念品的销售价,使旅游部门销售该纪念品的月平均利润最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com