
【题目】已知函数![]() 在
在![]() 处的导数为
处的导数为![]() ,
,![]() ,
,
(1)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(2)若![]() 在
在![]() 上有且只有一个零点,求
上有且只有一个零点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由![]() ,求出
,求出![]() ,当
,当![]() 时,易知不等式成立;当
时,易知不等式成立;当![]() 时,
时,![]() 恒成立可转化为
恒成立可转化为![]() 恒成立,令
恒成立,令![]() ,求导判断
,求导判断![]() 的单调性,求出最小值,即可得到
的单调性,求出最小值,即可得到![]() 的取值范围;
的取值范围;
(2)由(1)知,![]() ,从而
,从而![]() ,因为函数
,因为函数![]() 为偶函数,且
为偶函数,且![]() ,所以要使
,所以要使![]() 在
在![]() 上有且只有一个零点,只需
上有且只有一个零点,只需![]() 时,
时,![]() 和
和![]() 没有交点,对
没有交点,对![]() 、
、![]() 、
、![]() 三种情况分类讨论,可得
三种情况分类讨论,可得![]() 的取值范围.
的取值范围.
(1)由题意,![]() ,由
,由![]() ,解得
,解得![]() ,
,
所以![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ,不等式成立,
,不等式成立,
②当![]() 时,
时,![]() 恒成立可转化为
恒成立可转化为![]() 恒成立,
恒成立,
令![]() ,
,![]() ,
,
![]() ,
,
令![]() ,则
,则![]() ,
,
因为![]() ,所以
,所以![]() 恒成立,
恒成立,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
又![]() 时,
时,![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
所以![]() ;
;
(2)由(1)知,![]() ,
,
所以![]() ,
,
则![]() ,
,
所以![]() 是偶函数,且
是偶函数,且![]() ,
,
所以要使![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,
只需![]() 时,
时,![]() 和
和![]() 没有交点.
没有交点.
①当![]() 时,
时,![]() ,
,
![]() ,解得
,解得![]() ,
,![]() ,不成立;
,不成立;
②当![]() 时,
时,![]() 和
和![]() 的图象如图1所示,
的图象如图1所示,
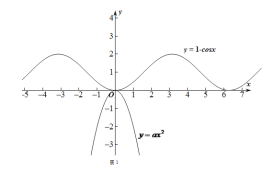
由图像知,当![]() 时,
时,![]() 和
和![]() 相交于原点,
相交于原点,
![]() 和
和![]() 只有一个交点,故
只有一个交点,故![]() 时成立;
时成立;
③当![]() 时,
时,![]() 和
和![]() 的图象如图2所示,
的图象如图2所示,
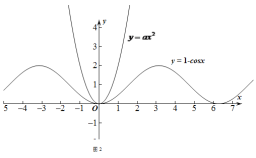
有图象知,要使![]() 和
和![]() 只有一个交点,
只有一个交点,
则对任意![]() ,有
,有![]()
![]()
![]() ,即
,即![]() ,
,
即![]() 在
在![]() 恒成立,
恒成立,
![]() ,当
,当![]() 时,
时,![]() 恒成立,
恒成立,
所以![]() 即
即![]() 在
在![]() 单调递增,
单调递增,![]() ,
,
此时![]() 成立,
成立,![]() 符合题意,
符合题意,
当![]() 时,存在
时,存在![]() ,使得
,使得![]() 在
在![]() 上递减,此时
上递减,此时![]() ,不合题意,
,不合题意,
综上所述,当![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆Γ:![]() 的左,右焦点分别为F1(
的左,右焦点分别为F1(![]() ,0),F2(
,0),F2(![]() ,0),椭圆的左,右顶点分别为A,B,已知椭圆Γ上一异于A,B的点P,PA,PB的斜率分别为k1,k2,满足
,0),椭圆的左,右顶点分别为A,B,已知椭圆Γ上一异于A,B的点P,PA,PB的斜率分别为k1,k2,满足![]() .
.
(1)求椭圆Γ的标准方程;
(2)若过椭圆Γ左顶点A作两条互相垂直的直线AM和AN,分别交椭圆Γ于M,N两点,问x轴上是否存在一定点Q,使得∠MQA=∠NQA成立,若存在,则求出该定点Q,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“众志成城,抗击疫情,一方有难,八方支援”,在此次抗击疫情过程中,各省市都派出援鄂医疗队. 假设汕头市选派![]() 名主任医生,
名主任医生,![]() 名护士,组成三个医疗小组分配到湖北甲、乙、丙三地进行医疗支援,每个小组包括
名护士,组成三个医疗小组分配到湖北甲、乙、丙三地进行医疗支援,每个小组包括![]() 名主任医生和
名主任医生和![]() 名护士,则不同的分配方案有( )
名护士,则不同的分配方案有( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为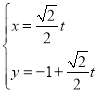 (t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为
(t为参数),以原点O为极点,x正半轴为极轴建立极坐标系,曲线的极坐标方程为![]() .
.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设P(0,-1),直线l与C的交点为M,N,线段MN的中点为Q,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com