
【题目】已知函数f(x)=loga(ax2-x+1)(a>0,a≠1).
(1) 若a=![]() ,求函数f(x)的值域.
,求函数f(x)的值域.
(2) 当f(x)在区间![]() 上为增函数时,求a的取值范围.
上为增函数时,求a的取值范围.
【答案】(1)(-∞,1].(2)![]() ∪[2,+∞).
∪[2,+∞).
【解析】试题分析:(1)先确定y=![]() x2-x+1范围为
x2-x+1范围为![]() ,再根据对数函数单调性确定函数值域(-∞,1].(2)由复合函数单调性依次讨论:若a>1,则y=ax2-x+1在区间
,再根据对数函数单调性确定函数值域(-∞,1].(2)由复合函数单调性依次讨论:若a>1,则y=ax2-x+1在区间![]() 上为增函数,结合二次函数对称轴得
上为增函数,结合二次函数对称轴得![]() ,解得 a≥2;② 若0<a<1,则y=ax2-x+1在区间
,解得 a≥2;② 若0<a<1,则y=ax2-x+1在区间![]() 上为减函数,结合二次函数对称轴以及定义区间得
上为减函数,结合二次函数对称轴以及定义区间得![]() ,且
,且![]() ,解得
,解得![]()
试题解析: 解:(1) 若a=![]() ,则f(x)=log0.5
,则f(x)=log0.5![]() =log0.5[
=log0.5[![]() (x-1)2+
(x-1)2+![]() ]≤log0.5
]≤log0.5![]() =1,
=1,
所以a=![]() 时,函数f(x)的值域是(-∞,1].
时,函数f(x)的值域是(-∞,1].
(2) ① 若a>1,要f(x)在区间![]() 上为增函数,只要
上为增函数,只要![]() ≤
≤![]() 且
且![]() a-
a-![]() +1>0,解得a≥2;
+1>0,解得a≥2;
② 若0<a<1,要f(x)在区间[![]() ,
,![]() ]上为增函数,只要
]上为增函数,只要![]() ≥
≥![]() 且
且![]() a-
a-![]() +1>0,解得
+1>0,解得![]() <a≤
<a≤![]() .
.
综上所述,所求a的取值范围是(![]() ,
,![]() ]∪[2,+∞).
]∪[2,+∞).


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知AD=4, ![]() ,AB=2CD=8.
,AB=2CD=8.
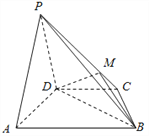
(1)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)当M点位于线段PC什么位置时,PA∥平面MBD?
查看答案和解析>>
科目:高中数学 来源: 题型:
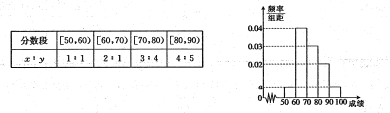
【题目】某校100名学生其中考试语文成绩的频率分布直方图所示,其中成绩分组区间是:
![]() .
.
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示,
之比如下表所示,
求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足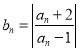 ,其中
,其中![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() .
.
(B)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
, ![]() .
.
(1)求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并猜想
,并猜想![]() 的表达式(不必写出证明过程);
的表达式(不必写出证明过程);
(2)设![]() ,
, ![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:
(单位: ![]() )满足关系
)满足关系![]() ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值。
达到最小,并求最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
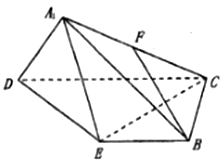
【题目】已知平行四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,且△
的中点,且△![]() 是等边三角形,沿
是等边三角形,沿![]() 把△
把△![]() 折起至
折起至![]() 的位置,使得
的位置,使得![]() .
.
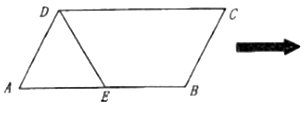
(1)![]() 是线段
是线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,以
,以![]() 为圆心,椭圆的短半轴长为半径的圆与直线
为圆心,椭圆的短半轴长为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,和平面内一点
,和平面内一点![]() (
(![]() ),过点
),过点![]() 任作直线
任作直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,设直线
两点,设直线![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,试求
,试求![]() ,
,![]() 满足的关系式.
满足的关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com