
已知 为实数,
为实数, :点
:点 在圆
在圆 的内部;
的内部;  :
: 都有
都有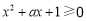 .
.
(1)若 为真命题,求
为真命题,求 的取值范围;
的取值范围;
(2)若 为假命题,求
为假命题,求 的取值范围;
的取值范围;
(3)若“ 且
且 ”为假命题,且“
”为假命题,且“ 或
或 ”为真命题,求
”为真命题,求 的取值范围.
的取值范围.
(1) 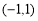 ;(2
;(2 )
)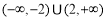 ;(3)
;(3)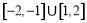 .
.
【解析】
试题分析:(1)关键在于根据点与圆的位置关系的结论得到不等式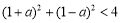 ;
;
(2)关键在于由一元二次函数,一元二次不等式,一元二次方程的知识可知,若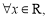 都有
都有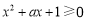 ,则对应的二次函数开口向上,二次方程的判别式
,则对应的二次函数开口向上,二次方程的判别式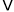 ≤0;
≤0;
(3)由简易逻辑知识可知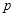 与
与 一真一假,然后利用集合的运算和解不等式组知识即可解决.
一真一假,然后利用集合的运算和解不等式组知识即可解决.
试题解析:(1)由题意得,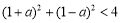 ,解得
,解得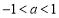 ,
,
故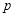 为真命题时
为真命题时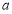 的取值范围为
的取值范围为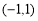 . 4分
. 4分
(2)若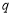 为真命题,则
为真命题,则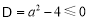 ,解得
,解得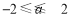 ,
,
故 为假命题时
为假命题时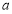 的取值范围
的取值范围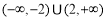 . 8分
. 8分
(3)由题意得,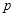 与
与 一真一假,从而
一真一假,从而
当 真
真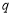 假时有
假时有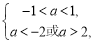 无解; 10分
无解; 10分
当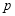 假
假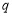 真时有
真时有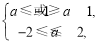 解得
解得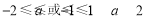 . 12分
. 12分
∴实数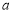 的取值范围是
的取值范围是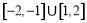 . 14分
. 14分
考点:(1) 点与圆的位置关系;(2)三个一元二次的关系;(3)简易逻辑;(4)集合的运算.


科目:高中数学 来源:2015届江西南昌市四校高二上学期期末联考理科数学试卷(解析版) 题型:选择题
若直线L的参数方程为 为参数),则直线L的倾斜角的余弦值为( )
为参数),则直线L的倾斜角的余弦值为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省常州市高二上学期期末考试文科数学试卷(解析版) 题型:解答题
已知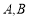 分别是椭圆
分别是椭圆 的左,右顶点,点
的左,右顶点,点 在椭圆
在椭圆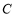 上,且直线
上,且直线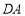 与直线
与直线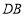 的斜率之积为
的斜率之积为 .
.

(1)求椭圆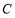 的标准方程;
的标准方程;
(2)点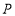 为椭圆
为椭圆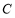 上除长轴端点外的任一点,直线
上除长轴端点外的任一点,直线 ,
,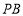 与椭圆的右准线分别交于点
与椭圆的右准线分别交于点 ,
, .
.
①在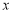 轴上是否存在一个定点
轴上是否存在一个定点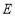 ,使得
,使得 ?若存在,求点
?若存在,求点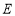 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
②已知常数 ,求
,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省常州市高二上学期期末考试文科数学试卷(解析版) 题型:填空题
“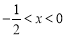 ”是“不等式
”是“不等式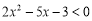 成立”的 条件(在“充分不必要”, “必要不充分”, “充要”, “既不充分又不必要”中选一个填写).
成立”的 条件(在“充分不必要”, “必要不充分”, “充要”, “既不充分又不必要”中选一个填写).
查看答案和解析>>
科目:高中数学 来源:2015届江苏扬州市高二第一学期期末调研考试数学试卷(解析版) 题型:填空题
先后抛掷一枚质地均匀的骰子(各面上分别标有点数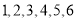 )两次,骰子朝上的面的点数依次记为
)两次,骰子朝上的面的点数依次记为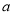 和
和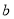 ,则双曲线
,则双曲线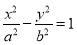 为等轴双曲线的概率为 .
为等轴双曲线的概率为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com