
【题目】已知函数![]() ,
,![]()
(1)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 和
和![]() 的图像有两个交点,它们的横坐标分别为
的图像有两个交点,它们的横坐标分别为![]() ,求证:
,求证:![]()
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)先对函数求导,得到![]() ,求出
,求出![]() ,
,![]() ,进而可得出结果;
,进而可得出结果;
(2)先令![]() ,对函数求导,得到
,对函数求导,得到![]() ,分别讨论
,分别讨论![]() ,
,![]() ,
,![]() 三种情况,用导数研究函数单调性,最值等,即可证明结论成立.
三种情况,用导数研究函数单调性,最值等,即可证明结论成立.
(1)因为![]() ,
,
所以![]() ,
,
所以![]() ,又
,又![]() ,
,
所以切线方程为:![]() ,即
,即![]() .
.
(2)令![]() ,依题意
,依题意![]() 有两个零点.
有两个零点.
又![]() ,
,
①当![]() ,则
,则![]() ,
,![]() 只有一个零点,
只有一个零点,
②当![]() ,由
,由![]() 得
得![]() 或
或![]() .
.
若![]() ,则
,则![]() ,故当
,故当![]() 时,
时,![]() ,
,
因此![]() 在
在![]() 上单调递增.
上单调递增.
又当![]() 时,
时,![]() ,所以
,所以![]() 不存在两个零点.
不存在两个零点.
若![]() ,则
,则![]() ,故当
,故当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
因此![]() 在
在![]() 单调递减,在
单调递减,在![]() )单调递增.
)单调递增.
又当![]() 时,
时,![]() ,所以
,所以![]() 不存在两个零点.
不存在两个零点.
③当![]() ,则当
,则当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
又![]() ,
,![]() ,取
,取![]() 满足
满足![]() 且
且![]() ,
,
则![]() ,
,
故![]() 存在两个零点;
存在两个零点;
不妨设![]() ,由③知
,由③知![]() ,
,![]() ,
,![]() ,
,![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 等价于
等价于![]() ,即
,即![]() .
.
由于![]() ,而
,而![]() ,
,
所以![]() .
.
设![]() ,则
,则![]() .
.
所以当![]() 时,
时,![]() ,而
,而![]() ,故当
,故当![]() 时,
时,![]() .
.
从而![]() ,故
,故![]()


科目:高中数学 来源: 题型:
【题目】焦点在![]() 轴上的椭圆
轴上的椭圆![]() 经过点
经过点![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() .
.![]() ,
,![]() 是椭圆的左、右焦点,
是椭圆的左、右焦点,![]() 为椭圆上任意点.
为椭圆上任意点.
(1)若![]() 面积为
面积为![]() ,求
,求![]() 的值;
的值;
(2)若点![]() 为
为![]() 的中点(
的中点(![]() 为坐标原点),过
为坐标原点),过![]() 且平行于
且平行于![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,是否存在实数
两点,是否存在实数![]() ,使得
,使得![]() ;若存在,请求出
;若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() ,
,![]() ,都有
,都有![]() ,
,![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“速增函数”.
为“速增函数”.
(1)试判断函数![]() 与
与![]() 是否是“速增函数”;
是否是“速增函数”;
(2)若函数![]() 为“速增函数”,求
为“速增函数”,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 为“速增函数”,且
为“速增函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,![]() 是某海湾旅游区的一角,其中
是某海湾旅游区的一角,其中![]() ,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸
,为了营造更加优美的旅游环境,旅游区管委会决定在直线海岸![]() 和
和![]() 上分别修建观光长廊
上分别修建观光长廊![]() 和AC,其中
和AC,其中![]() 是宽长廊,造价是
是宽长廊,造价是![]() 元/米,
元/米,![]() 是窄长廊,造价是
是窄长廊,造价是![]() 元/米,两段长廊的总造价为120万元,同时在线段
元/米,两段长廊的总造价为120万元,同时在线段![]() 上靠近点
上靠近点![]() 的三等分点
的三等分点![]() 处建一个观光平台,并建水上直线通道
处建一个观光平台,并建水上直线通道![]() (平台大小忽略不计),水上通道的造价是
(平台大小忽略不计),水上通道的造价是![]() 元/米.
元/米.
(1) 若规划在三角形![]() 区域内开发水上游乐项目,要求
区域内开发水上游乐项目,要求![]() 的面积最大,那么
的面积最大,那么![]() 和
和![]() 的长度分别为多少米?
的长度分别为多少米?
(2) 在(1)的条件下,建直线通道![]() 还需要多少钱?
还需要多少钱?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )
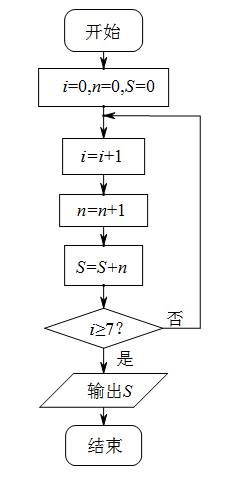
A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为正数的数列{an}的首项![]() ,前n项和为Sn,且Sn+1+Sn=λ
,前n项和为Sn,且Sn+1+Sn=λ![]() ..
..
(1)求{an}的通项公式;
(2)若数列{bn}满足bn=λnan,求{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com