
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值和最小值;
上的最大值和最小值;
(2)若函数![]() 为
为![]() 上的单调函数,求实数
上的单调函数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)由![]() 得
得![]() ,对其求导,得到
,对其求导,得到![]() ,解对应不等式,求出单调区间,进而可求出最值;
,解对应不等式,求出单调区间,进而可求出最值;
(2)先由![]() 得到函数
得到函数![]() 不可能在
不可能在![]() 上单调递增,由题意,得到
上单调递增,由题意,得到![]() 在
在![]() 上单调递减,推出
上单调递减,推出![]() 恒成立;令
恒成立;令![]() ,用导数的方研究其单调性,进而可求出结果.
,用导数的方研究其单调性,进而可求出结果.
(1)当![]() 时,
时,![]() ,所以
,所以![]() .
.
由![]() 解得
解得![]() ,由
,由![]() 解得
解得![]() .
.
故函数![]() 在区间
在区间![]() 上单减,在区间
上单减,在区间![]() 上单增.
上单增.
![]() ,
,
![]() ,
,![]() ;
;
(2) 因为![]() ,所以函数
,所以函数![]() 不可能在
不可能在![]() 上单调递增.
上单调递增.
所以,若函数![]() 为
为![]() 上单调函数,则必是单调递减函数,即
上单调函数,则必是单调递减函数,即![]() 恒成立.
恒成立.
由![]() 可得
可得![]() ,
,
故![]() 恒成立的必要条件为
恒成立的必要条件为![]() .
.
令![]() ,则
,则![]() .
.
当![]() 时,由
时,由![]() ,可得
,可得![]() ,
,
由![]() 可得
可得![]() ,
,
![]() 在
在![]() .上单调递增,在
.上单调递增,在![]() 上单调递减.
上单调递减.
故![]()
令![]() ,下证:当
,下证:当![]() 时,
时,![]() .
.
即证![]() ,令
,令![]() ,其中
,其中![]() ,则
,则![]() ,
,
则原式等价于证明:当![]() 时,
时,![]() .
.
由(1)的结论知,显然成立.
综上,当![]() 时,函数
时,函数![]() 为
为![]() 上的单调函数,且单调递减.
上的单调函数,且单调递减.


科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() 若满足:①对任意
若满足:①对任意![]() 、
、![]() ,都有
,都有![]() ;②对任意
;②对任意![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“中心捺函数”,其中点
为“中心捺函数”,其中点![]() 称为函数
称为函数![]() 的中心.已知函数
的中心.已知函数![]() 是以
是以![]() 为中心的“中心捺函数”,若满足不等式
为中心的“中心捺函数”,若满足不等式![]() ,当
,当![]() 时,
时,![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了丰富学生活动,在体育课上,体育教师设计了一个游戏,让甲、乙、丙三人各抓住橡皮带的一端,甲站在直角![]() 斜边
斜边![]() 的中点
的中点![]() 处,乙站在
处,乙站在![]() 处,丙站在
处,丙站在![]() 处.游戏开始,甲不动,乙、丙分别以
处.游戏开始,甲不动,乙、丙分别以![]() 和
和![]() 的速度同时出发,匀速跑向终点
的速度同时出发,匀速跑向终点![]() 和
和![]() ,运动过程中绷紧的橡皮带围成一个如图所示的
,运动过程中绷紧的橡皮带围成一个如图所示的![]() .(规定:只要有一人跑到终点,游戏就结束,且
.(规定:只要有一人跑到终点,游戏就结束,且![]() ).已知
).已知![]() 长为
长为![]() ,
,![]() 长为
长为![]() ,记经过
,记经过![]() 后
后![]() 的面积为
的面积为![]() .
.
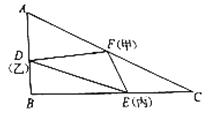
(1)求![]() 关于
关于![]() 的函数表示,并求出
的函数表示,并求出![]() 的取值范围;
的取值范围;
(2)当游戏进行到![]() 时,体育教师宣布停止,求此时
时,体育教师宣布停止,求此时![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() ,
,![]() 是曲线
是曲线![]() 上的任意一点,动点
上的任意一点,动点![]() 满足
满足![]()
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)经过点![]() 的动直线
的动直线![]() 与点
与点![]() 的轨迹方程交于
的轨迹方程交于![]() 两点,在
两点,在![]() 轴上是否存在定点
轴上是否存在定点![]() (异于点
(异于点![]() ),使得
),使得![]() ?若存在,求出
?若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系中的坐标原点为极点,![]() 轴的正半抽为极轴,建立极坐标系,曲线
轴的正半抽为极轴,建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】安徽怀远石榴(Punicagranatum)自古就有“九州之奇树,天下之名果”的美称,今年又喜获丰收.怀远一中数学兴趣小组进行社会调查,了解到某石榴合作社为了实现![]() 万元利润目标,准备制定激励销售人员的奖励方案:在销售利润超过
万元利润目标,准备制定激励销售人员的奖励方案:在销售利润超过![]() 万元时,按销售利润进行奖励,且奖金
万元时,按销售利润进行奖励,且奖金![]() (单位:万元)随销售利润
(单位:万元)随销售利润![]() (单位:万元)的增加而增加,但奖金总数不超过
(单位:万元)的增加而增加,但奖金总数不超过![]() 万元,同时奖金不能超过利润的
万元,同时奖金不能超过利润的![]() .同学们利用函数知识,设计了如下函数模型,其中符合合作社要求的是( )(参考数据:
.同学们利用函数知识,设计了如下函数模型,其中符合合作社要求的是( )(参考数据:![]() )
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com