练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在2019年亚洲杯前，某商家为了鼓励中国球迷组团到阿联酋支持中国队，制作了3种精美海报，每份中国队球迷礼包中随机装入一份海报，每集齐3种不同的海报就可获得中国队在亚洲杯上所有比赛中的1张门票．现有6名中国队球迷组成的球迷团，每人各买一份中国队球迷礼包，则该球迷团至少获得1张门票的可能情况的种数为（ ）

    A.360B.450C.540D.990

    【答案】C

    【解析】

    由题可知：当3种海报的数量分别为2，2，2时，该球迷团可获得2张门票；当3种海报的数量分别为3，2，1或3种海报的数量分别为4，1，1时，该球迷团可获得1张门票，分别计算各个情况的结果，再求和即可得答案.

    由题意可知，该球迷团最多可获得2张门票，若3种海报的数量分别为2，2，2，则不同的情况种数为；若3种海报的数量分别为3，2，1，则不同的情况种数为；若3种海报的数量分别为4，1，1，则不同的情况种数为．

    故该球迷团至少获得1张门票的可能情况的种数为．

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图所示，在三棱锥中，，，，点为中点．

    （1）求证：平面平面；

    （2）若点为中点，求平面与平面所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】根据以往统计资料，某地车主购买甲种保险的概率为0.4，购买乙种保险但不购买甲种保险的概率为0.2.设各车主购买保险相互独立.

    （1）求该地1位车主至少购买甲乙两种保险中的1种的概率；

    （2）求该地3位车主中恰有1位车主甲乙两种保险都不购买的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某保险公司为客户定制了5个险种：甲，一年期短险；乙，两全保险；丙，理财类保险；丁，定期寿险：戊，重大疾病保险，各种保险按相关约定进行参保与理赔.该保险公司对5个险种参保客户进行抽样调查，得出如下的统计图例，以下四个选项错误的是（ ）

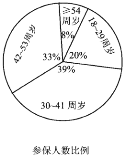
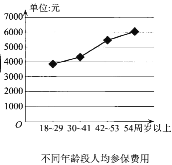
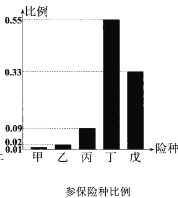
    A.54周岁以上参保人数最少B.18～29周岁人群参保总费用最少

    C.丁险种更受参保人青睐D.30周岁以上的人群约占参保人群的80%

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数．

    （1）求的单调区间；

    （2）在函数的图象上取两个不同的点，令直线的斜率为，则在函数的图象上是否存在点，且，使得？若存在，求两点的坐标，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若数列满足，且存在常数，使得对任意的都有，则称数列为“k控数列”．

    （1）若公差为d的等差数列是“2控数列”，求d的取值范围；

    （2）已知公比为的等比数列的前n项和为，数列与都是“k控数列”，求q的取值范围（用k表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数的单调减区间；

    （2）若不等式对恒成立，求实数的取值范围；

    （3）当时，试问过点可作的几条切线？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某综艺节目为比较甲、乙两名选手的各项能力（指标值满分为5分，分值高者为优），分别绘制了如图所示的六维能力雷达图，图中点A表示甲的创造力指标值为4，点B表示乙的空间能力指标值为3，则下列叙述错误的是（ ）

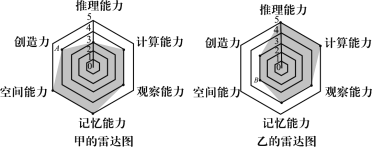
    A.甲的六大能力中推理能力最差B.甲的创造力优于观察能力

    C.乙的计算能力优于甲的计算能力D.乙的六大能力整体水平低于甲

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在棱长为1的正方体ABCD﹣A1B1C1D1中，点M，N分别是棱B1C1，C1D1的中点，过A，M，N三点作正方体的截面，将截面多边形向平面ADD1A1作投影，则投影图形的面积为_____．

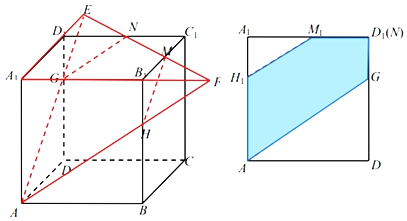
    查看答案和解析>>

    同步练习册答案