Question

【题目】已知函数f（x）=lnx+（e﹣a）x﹣b，其中e为自然对数的底数．若不等式f（x）≤0恒成立，则 的最小值为 ．

Answer 1

【答案】﹣
【解析】解：∵函数f（x）=lnx+（e﹣a）x﹣b，其中e为自然对数的底数， ∴ ，x＞0，
当a≤e时，f′（x）＞0，
f（x）在（0，+∞）上是增函数，∴f（x）≤0不可能恒成立，
当a＞e时，由 ，得x= ，
∵不等式f（x）≤0恒成立，∴f（x）的最大值为0，
当x∈（0， ）时，f′（x）＞0，f（x）单调递增，
当x∈（ ，+∞）时，f′（x）＜0，f（x）单调递减，
∴当x= 时，f（x）取最大值，
f（ ）=﹣ln（a﹣e）﹣b﹣1≤0，
∴ln（a﹣e）+b+1≥0，
∴b≥﹣1﹣ln（a﹣e），
∴ （a＞e），
令F（x）= ，x＞e，
F′（x）= = ，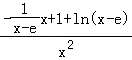
令H（x）=（x﹣e）ln（x﹣e）﹣e，
H′（x）=ln（x﹣e）+1，
由H′（x）=0，得x=e+ ，
当x∈（e+ ，+∞）时，H′（x）＞0，H（x）是增函数，
x∈（e，e+ ）时，H′（x）＜0，H（x）是减函数，
∴当x=e+ 时，H（x）取最小值H（e+ ）=﹣e﹣ ，
∵x→e时，H（x）→0，x＞2e时，H（x）＞0，H（2e）=0，
∴当x∈（e，2e）时，F′（x）＜0，F（x）是减函数，
当x∈（2e，+∞）时，F′（x）＞0，F（x）是增函九，
∴x=2e时，F（x）取最小值，F（2e）= =﹣ ，
∴ 的最小值为﹣ ．
故答案为：﹣ ．
求出 ，x＞0，当a≤e时，f′（x）＞0，f（x）≤0不可能恒成立，当a＞e时，由 ，得x= ，由题意当x= 时，f（x）取最大值0，推导出 （a＞e），令F（x）= ，x＞e，F′（x）= ，令H（x）=（x﹣e）ln（x﹣e）﹣e，H′（x）=ln（x﹣e）+1，由此利用导数性质能求出 的最小值．