
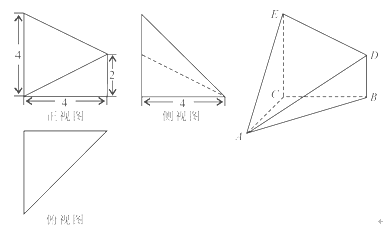
已知几何体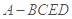 的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求异面直线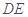 与
与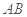 所成角的余弦值;
所成角的余弦值;
(2)求二面角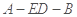 的正弦值;
的正弦值;
(3)求此几何体的体积的大小
(1) 异面直线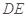 与
与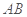 所成的角的余弦值为
所成的角的余弦值为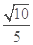 .
.
(2) 二面角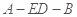 的的正弦值为
的的正弦值为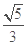 .
.
(3)几何体的体积为16.
【解析】
试题分析:(1) 先确定几何体中的棱长, 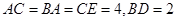 ,通过取
,通过取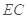 的中点
的中点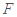 ,连结
,连结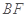 ,
,
则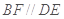 ,∴
,∴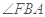 或其补角即为异面直线
或其补角即为异面直线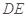 与
与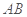 所成的角. 在
所成的角. 在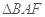 中即可解得
中即可解得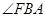 的余弦值.
的余弦值.
(2) 因为二面角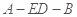 的棱为
的棱为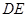 ,可通过三垂线法找二面角,由已知
,可通过三垂线法找二面角,由已知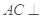 平面
平面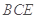 ,过
,过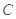 作
作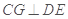 交
交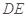 于
于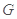 ,连
,连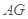 .可得
.可得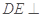 平面
平面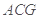 ,从而
,从而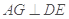 ,∴
,∴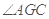 为二面角
为二面角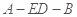 的平面角. 在
的平面角. 在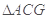 中可解得
中可解得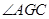 角的正弦值.
角的正弦值.
(3)该几何体是以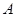 为顶点,
为顶点,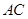 为高的,
为高的,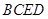 为底的四棱锥,所以
为底的四棱锥,所以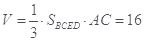
此外也可以以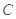 为原点,以
为原点,以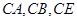 所在直线为
所在直线为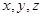 轴建立空间直角坐标系来解答.
轴建立空间直角坐标系来解答.
试题解析:(1)取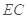 的中点是
的中点是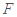 ,连结
,连结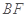 ,
,
则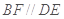 ,∴
,∴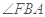 或其补角即为异面直线
或其补角即为异面直线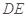 与
与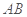 所成的角.
所成的角.
在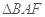 中,
中,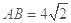 ,
,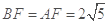 .∴
.∴ .
.
∴异面直线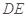 与
与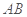 所成的角的余弦值为
所成的角的余弦值为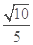 .
.
(2)因为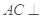 平面
平面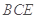 ,过
,过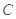 作
作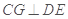 交
交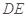 于
于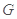 ,连
,连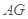 .
.
可得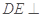 平面
平面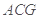 ,从而
,从而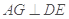 ,
,
∴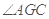 为二面角
为二面角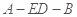 的平面角.
的平面角.
在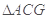 中,
中,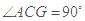 ,
,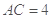 ,
,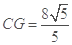 ,
,
∴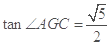 .∴
.∴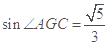 .
.
∴二面角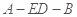 的的正弦值为
的的正弦值为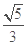 .
.
(3)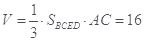 ,∴几何体的体积为16.
,∴几何体的体积为16.
方法2:(1)以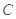 为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
为原点,以CA,CB,CE所在直线为x,y,z轴建立空间直角坐标系.
则A(4,0,0),B(0,4,0),D(0,4,2),E(0,0,4)
 ,
,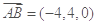 ,∴
,∴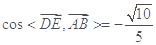 ,
,
∴异面直线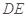 与
与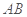 所成的角的余弦值为
所成的角的余弦值为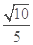 .
.
(2)平面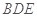 的一个法向量为
的一个法向量为 ,设平面ADE的一个法向量为
,设平面ADE的一个法向量为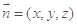 ,
,
所以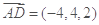 ,
, ,
,
则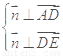 ,
∴
,
∴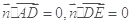
从而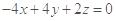 ,
,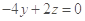 ,
,
令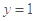 ,则
,则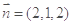 ,
,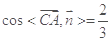 ,
,
∴二面角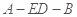 的的正弦值为
的的正弦值为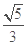 .
.
(3)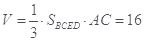 ,∴几何体的体积为16.
,∴几何体的体积为16.
考点:1、三视图还原几何体的棱长;2、异面直线所成的角,二面角;3、四棱锥的体积;4、利用向量法解立体几何问题.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com