
【题目】某地区工会利用“健步行![]() ” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分), 每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了 1000名会员,统计了当天他们的步数,并将样本数据分为
” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分), 每多走2千步再积20分(不足2千步不积分).为了解会员的健步走情况,工会在某天从系统中随机抽取了 1000名会员,统计了当天他们的步数,并将样本数据分为![]() ,
,![]() 九组,整理得到如图频率分布直方图:
九组,整理得到如图频率分布直方图:
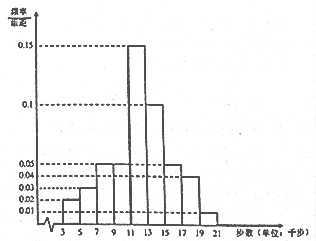
(1)求当天这1000名会员中步数少于11千步的人数;
(2)从当天步数在![]() 的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
的会员中按分层抽样的方式抽取6人,再从这6人中随机抽取2人,求这2人积分之和不少于200分的概率;
(3)写出该组数据的中位数(只写结果).
【答案】(1)300(2)![]() (3)
(3)![]()
【解析】分析:(1)根据直方图的性质,求出每个小矩形的面积可得到健步走的步数在![]() 内的频率,
内的频率,
健步走的步数在![]() 内的频率,健步走的步数在
内的频率,健步走的步数在![]() 内的频率,健步走的步数在
内的频率,健步走的步数在![]() 内的频率,从而可得结果;(2)按分层抽样的方法,在
内的频率,从而可得结果;(2)按分层抽样的方法,在![]() 内应抽取3人,在
内应抽取3人,在![]() 内应抽取2人,在
内应抽取2人,在![]() 内应抽取1人,利用列举法
内应抽取1人,利用列举法![]() 人中任意选取
人中任意选取![]() 人共有
人共有![]() 种,其中这2人的积分之和不少于
种,其中这2人的积分之和不少于![]() 的情况共有
的情况共有![]() 种,由古典概型概率公式可得结果;(3)根据频率分布直方图的性质能求出中位数.
种,由古典概型概率公式可得结果;(3)根据频率分布直方图的性质能求出中位数.
详解:(Ⅰ)这1000名会员中健步走的步数在![]() 内的人数为
内的人数为![]() ;
;
健步走的步数在![]() 内的人数为
内的人数为![]() ;
;
健步走的步数在![]() 内的人数为
内的人数为![]() ;
;
健步走的步数在![]() 内的人数为
内的人数为![]() ;
;
![]() .
.
所以这1000名会员中健步走的步数少于11千步的人数为300人.
(Ⅱ)按分层抽样的方法,在![]() 内应抽取3人,记为
内应抽取3人,记为![]() ,
,![]() ,
,![]() ,每人的积分是90分;在
,每人的积分是90分;在![]() 内应抽取2人,记为
内应抽取2人,记为![]() ,
,![]() ,每人的积分是110分;
,每人的积分是110分;
在![]() 内应抽取1人,记为
内应抽取1人,记为![]() ,每人的积分是130分;
,每人的积分是130分;
从6人中随机抽取2人,有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共15种方法.
共15种方法.
所以从6人中随机抽取2人,这2人的积分之和不少于200分的有![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共12种方法.
共12种方法.
设从6人中随机抽取2人,这2人的积分之和不少于200分为事件![]() ,则
,则
![]() .
.
所以从6人中随机抽取2人,这2人的积分之和不少于200分的概率为![]() .
.
(Ⅲ)中位数为![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某校从参加高一年级期中考试的学生中随机抽出60名学生,将其物理成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,观察图形的信息,回答下列问题:
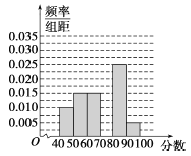
(1)求分数在[70,80)内的频率,并补全这个频率分布直方图;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计本次考试中的平均分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|2x﹣a|+|x﹣1|,a∈R.
(Ⅰ)若不等式f(x)≥2﹣|x﹣1|恒成立,求实数a的取值范围;
(Ⅱ)当a=1时,直线y=m与函数f(x)的图象围成三角形,求m的最大值及此时围成的三角形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() :
: ![]() ,右顶点为
,右顶点为 ![]() ,离心率为
,离心率为 ![]() ,直线
,直线 ![]() :
: ![]() 与椭圆
与椭圆 ![]() 相交于不同的两点
相交于不同的两点 ![]() ,
, ![]() ,过
,过 ![]() 的中点
的中点 ![]() 作垂直于
作垂直于 ![]() 的直线
的直线 ![]() ,设
,设 ![]() 与椭圆
与椭圆 ![]() 相交于不同的两点
相交于不同的两点 ![]() ,
, ![]() ,且
,且 ![]() 的中点为
的中点为 ![]() .
.
(Ⅰ)求椭圆 ![]() 的方程;
的方程;
(Ⅱ)设原点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() ,求
,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ![]() ,过点
,过点 ![]() 的直线
的直线 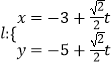 (
( ![]() 为参数)与曲线
为参数)与曲线 ![]() 相交于点
相交于点 ![]() ,
, ![]() 两点.
两点.
(1)求曲线 ![]() 的平面直角坐标系方程和直线
的平面直角坐标系方程和直线 ![]() 的普通方程;
的普通方程;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下关于命题的说法正确的有(填写所有正确命题的序号).
①“若 ![]() ,则函数
,则函数 ![]() (
( ![]() ,且
,且 ![]() )在其定义域内是减函数”是真命题;
)在其定义域内是减函数”是真命题;
②命题“若 ![]() ,则
,则 ![]() ”的否命题是“若
”的否命题是“若 ![]() ,则
,则 ![]() ”;
”;
③命题“若 ![]() ,
, ![]() 都是偶数,则
都是偶数,则 ![]() 也是偶数”的逆命题为真命题;
也是偶数”的逆命题为真命题;
④命题“若 ![]() ,则
,则 ![]() ”与命题“若
”与命题“若 ![]() ,则
,则 ![]() ”等价.
”等价.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com