练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知平行四边形 的三个顶点坐标为 ， ， .
    （Ⅰ）求顶点 的坐标；
    （Ⅱ）求四边形 的面积.

    【答案】解：(Ⅰ)如图，设 ，

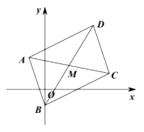
    因为四边形 为平行四边形，所以对角线互相平分，
    又 ， ，所以 ，
    又 ，所以顶点 的坐标为D .
    (Ⅱ)依题意可得 ，
    故直线 的方程为 ，即 ，
    又 ，
    点 到直线 的距离 .
    所以四边形 的面积
    【解析】（Ⅰ）根据题目中所给的条件的特点，设AC和BD相交于点M，因为四边形ABCD为平行四边形，所以对角线互相平分，利用中点坐标公式可得M，进而得到D的坐标．
    （Ⅱ）依题意可得直线BC的斜率，利用直线方程点斜式可得直线BC的方程，利用两点之间的距离公式可得|BC|的大小．利用点到直线的距离公式可得点A到直线BC的距离d，最后利用面积公式即可得出答案．考查了平行四边形的性质、点到直线的距离公式、中点坐标公式、四边形的面积，考查了推理能力与计算能力.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某地区工会利用“健步行” 开展健步走积分奖励活动.会员每天走5 千步可获积分30分(不足5千步不积分)， 每多走2千步再积20分（不足2千步不积分).为了解会员的健步走情况，工会在某天从系统中随机抽取了 1000名会员，统计了当天他们的步数，并将样本数据分为，九组，整理得到如图频率分布直方图：

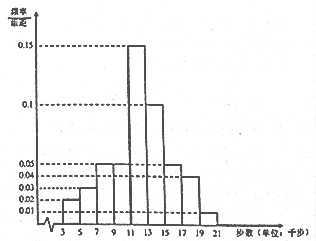
    （1）求当天这1000名会员中步数少于11千步的人数；

    （2）从当天步数在的会员中按分层抽样的方式抽取6人，再从这6人中随机抽取2人，求这2人积分之和不少于200分的概率；

    （3）写出该组数据的中位数（只写结果）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，曲线C1的参数方程为 （α为参数），直线C2的方程为y= ，以O为极点，以x轴正半轴为极轴建立极坐标系，
    （1）求曲线C1和直线C2的极坐标方程；
    （2）若直线C2与曲线C1交于A，B两点，求 + ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 ，设命题 ：指数函数 ≠ 在 上单调递增.命题 ：函数 的定义域为 ．若“ ”为假，“ ”为真，求 的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

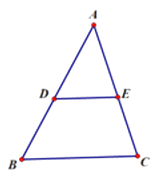
    【题目】如图，已知点 分别是Δ 的边 的中点，连接 .现将 沿 折叠至Δ 的位置,连接 .记平面 与平面 的交线为 ，二面角 大小为 .

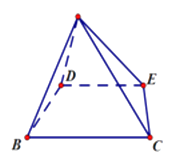
    （1）证明：
    （2）证明：
    （3）求平面 与平面 所成锐二面角大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，直四棱柱 的所有棱长均为2， 为 中点.

    （Ⅰ）求证： 平面 ；
    （Ⅱ）若 ，求平面 与平面 所成锐二面角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆 的两个焦点分别为 ， ，且经过点 .
    （Ⅰ）求椭圆 的标准方程；
    （Ⅱ） 的顶点都在椭圆 上，其中 关于原点对称，试问 能否为正三角形？并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知 .
    （Ⅰ）对一切 恒成立，求实数 的取值范围；
    （Ⅱ）证明：对一切 ，都有 成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数列中，若对任意都有（为常数）成立，则称为“等差比数列”，下面对“等差比数列” 的判断：①不可能为；②等差数列一定是等差比数列； ③等比数列一定是等差比数列 ；④通项公式为（其中，且，）的数列一定是等差比数列，其中正确的判断是（ ）

    A. ①③④ B. ②③④ C. ①④ D. ①③

    查看答案和解析>>

    同步练习册答案