【题目】求下列函数的值域：
（1）
；
（2）
；
（3）
（4）
；
（5）
；
（6）
.
【答案】（1）
；（2）
；（3）
；（4）
；（5）
；（6）
【解析】
（1）根据二次函数的值域求出被开方数的范围，即可求出函数的值域；
（2）根据二次函数的单调性，即可求出值域；
（3）分离常数，利用反比例函数的值域，即可求解；
（4）分离常数，利用二次函数的值域以及不等式的性质，即可求出函数值域；
（5）分类讨论去绝对值，转化为求一次函数的值域；
（6）利用二次函数的值域，结合不等式的性质，即可求出结论.
（1）
，
，函数
值域为；
（2）
，当
时单调递减，
当
时单调递增，
，
所以函数的值域是；
（3）
，
所以函数
的值域是；
（4）
，所以函数
值域是；
（5）
，当
时，
，
当
时，
，当
，
所以函数的值域是；
（6）
定义域为
且
，
，
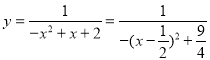或
，
或
，
所以函数的值域是.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】求满足下列条件的椭圆或双曲线的标准方程：
（1）椭圆的焦点在
轴上，焦距为4，且经过点
；
（2）双曲线的焦点在
轴上，右焦点为
，过作重直于轴的直线交双曲线于
，
两点，且
，离心率为
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
.
(1)求
的单调递增区间.
(2)在ΔABC中，角A，B，C所对的边分别为a，b，c，若f(A)=1，c=10，cosB=
，求ΔABC的中线AD的长.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f (x)＝x－(a＋1)ln x－
(a∈R)，g (x)＝
x2＋ex－xex.
（1）当x∈[1，e] 时，求f (x)的最小值；
（2）当a＜1时，若存在x1∈[e，e2]，使得对任意的x2∈[－2，0]，f (x1)＜g (x2)恒成立，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知直线
的参数方程为
(其中
为参数)，以坐标原点
为极点，以
轴正半轴为极轴，建立极坐标系，曲线
的极坐标方程为
（其中
）.
(1)若点
的直角坐标为
，且点
在曲线
内，求实数
的取值范围；
(2)若
,当
变化时，求直线
被曲线
截得的弦长的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校高三文科
名学生参加了
月份的高考模拟考试，学校为了了解高三文科学生的历史、地理学习情况，从名学生中抽取
名学生的成绩进行统计分析，抽出的名学生的地理、历史成绩如下表：
地理 历史 | [80,100] | [60,80） | [40,60） |
[80,100] | 8 | m | 9 |
[60,80） | 9 | n | 9 |
[40,60） | 8 | 15 | 7 |
若历史成绩在[80,100]区间的占30%，
（1）求
的值；
（2）请根据上面抽出的名学生地理、历史成绩，填写下面地理、历史成绩的频数分布表：
[80,100] | [60,80） | [40,60） | |
地理 | |||
历史 |
根据频数分布表中的数据估计历史和地理的平均成绩及方差（同一组数据用该组区间的中点值作代表），并估计哪个学科成绩更稳定.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某公司发放员工的薪水有三种方式：①第一个月工资3000元，以后每月以1%的增长率增长；②第一个月工资2400元，以后每月以2%的增长率增长；③第一个月工资为3200元，每月涨工资30元．
（1）设第x个月的工资分别为
元，试分别建立关于x的函数；
（2）借助计算器计算这三种情况下各个月的工资；
（3）请分析这三种领薪方法的区别，作为员工选择何种方法更合算？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
