
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线与圆![]() 相切,与椭圆
相切,与椭圆![]() 相交于
相交于![]() 两点,求证:
两点,求证:![]() 是定值.
是定值.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,在△MBC中,MA是BC边上的高,MA=3,AC=4,将△MBC沿MA进行翻折,使得∠BAC=90°如图,再过点B作BD∥AC,连接AD,CD,MD且![]() ,∠CAD=30°.
,∠CAD=30°.
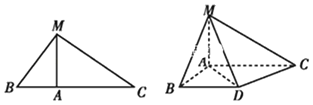
(1)求证:平面MCD⊥平面MAD;
(2)求点B到平面MAD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:f(x)=1+ax,在(0,2]上f(x)≥0恒成立,q函数g(x)=ax+2lnx在其定义域上存在极值.
(1)若p为真命题,求实数a的取值范围;
(2)如果“p∨q”为真命题,“p∧q”为假命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在圆锥![]() 中,已知高
中,已知高![]() ,底面圆的半径为4,
,底面圆的半径为4,![]() 为母线
为母线![]() 的中点;根据圆锥曲线的定义,下列四个图中的截面边界曲线分别为圆、椭圆、双曲线及抛物线,下面四个命题,正确的个数为( )
的中点;根据圆锥曲线的定义,下列四个图中的截面边界曲线分别为圆、椭圆、双曲线及抛物线,下面四个命题,正确的个数为( )

①圆的面积为![]() ;
;
②椭圆的长轴为![]() ;
;
③双曲线两渐近线的夹角为![]() ;
;
④抛物线中焦点到准线的距离为![]() .
.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() .
.
(1)求椭圆的方程;
(2)已知![]() ,是否存在
,是否存在![]() 使得点
使得点![]() 关于
关于![]() 的对称点
的对称点![]() (不同于点
(不同于点![]() )在椭圆
)在椭圆![]() 上?若存在求出此时直线
上?若存在求出此时直线![]() 的方程,若不存在说明理由.
的方程,若不存在说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入21世纪,互联网和通讯技术高速发展使商务进入一个全新的阶段,网上购物这一方便、快捷的购物形式已经被越来越多的人所接受![]() 某互联网公司为进一步了解大学生的网上购物的情况,对大学生的消费金额进行了调查研究,得到如下统计表:
某互联网公司为进一步了解大学生的网上购物的情况,对大学生的消费金额进行了调查研究,得到如下统计表:
组数 | 消费金额 | 人数 | 频率 |
第一组 |
| 1100 |
|
第二组 |
| 3900 |
|
第三组 |
| 3000 | p |
第四组 |
| 1200 |
|
第五组 | 不低于200元 | m |
|
![]() 求m,p的值;
求m,p的值;
![]() 该公司从参与调查且购物满150元的学生中采用分层抽样的方法抽取
该公司从参与调查且购物满150元的学生中采用分层抽样的方法抽取![]() 作为中奖用户,再随机抽取中奖用户的
作为中奖用户,再随机抽取中奖用户的![]() 获得一等奖
获得一等奖![]() 求第五组至少1人获得一等奖的概率.
求第五组至少1人获得一等奖的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com