[题目]已知圆C:2+2=2被y轴截得的线段AB与被直线y=3x+b所截得的线段CD的长度相等.则b等于( )A.± B.± C.±2 D.± 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知圆C：（x﹣1）2+（y﹣3）2=2被y轴截得的线段AB与被直线y=3x+b所截得的线段CD的长度相等，则b等于（）
A.±
B.±
C.±2
D.±

【答案】B
【解析】解：圆C：（x﹣1）2+（y﹣3）2=2的圆心C（1，3），半径r= ，

联立，得或，

∴圆C：（x﹣1）2+（y﹣3）2=2被y轴截得的线段AB的长为2，

∵圆C：（x﹣1）2+（y﹣3）2=2被y轴截得的线段AB与被直线y=3x+b所截得的线段CD的长度相等，

∴圆C：（x﹣1）2+（y﹣3）2=2被直线y=3x+b所截得的线段CD的长度为2，

∵圆心C（1，3）到直线y=3x+b的距离d= = ，

∴由勾股定理得：，

即2= ，解得b= ．

故选：B．

【考点精析】掌握直线与圆的三种位置关系是解答本题的根本，需要知道直线与圆有三种位置关系：无公共点为相离；有两个公共点为相交,这条直线叫做圆的割线；圆与直线有唯一公共点为相切，这条直线叫做圆的切线，这个唯一的公共点叫做切点．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=eax（a≠0）．
（1）当时，令（x＞0），求函数g（x）在[m，m+1]（m＞0）上的最小值；
（2）若对于一切x∈R，f（x）﹣x﹣1≥0恒成立，求a的取值集合；
（3）求证：．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知a和b是任意非零实数．
（1）求的最小值．
（2）若不等式|2a+b|+|2a﹣b|≥|a|（|2+x|+|2﹣x|）恒成立，求实数x的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，三棱柱ABC﹣A1B1C1中，侧棱AA1⊥底面A1B1C1 ， AA1=AC=BC=1，∠ACB=90°，D是A1B1的中点，F是BB1上的点，AB1 ， DF交于点E，且AB1⊥DF，则下列结论中不正确的是（）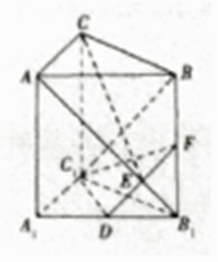
A.CE与BC1异面且垂直
B.AB1⊥C1F
C.△C1DF是直角三角形
D.DF的长为

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某学校有甲、乙两个实验班，为了了解班级成绩，采用分层抽样的方法从甲、乙两个班学生中分别抽取8名和6名测试他们的数学成绩与英语成绩（单位：分），用表示（m，n）．下面是乙班6名学生的测试分数：A（138，130），B（140，132），C（140，130），D（134，140），E（142，134），F（134，132），当学生的数学、英语成绩满足m≥135，且n≥130时，该学生定为优秀学生．
（1）已知甲班共有80名学生，用上述样本数据估计乙班优秀生的数量；
（2）从乙班抽出的上述6名学生中随机抽取3名，求至少有两名优秀生的概率；
（3）从乙班抽出的上述6名学生中随机抽取2名，其中优秀生数记为ξ，求ξ的分布列和数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】若函数f（x）= sin（2x+φ）（|φ|＜）的图象关于直线x= 对称，且当x1 ， x2∈（﹣ ，﹣ ），x1≠x2时，f（x1）=f（x2），则f（x1+x2）等于（）
A.
B.
C.
D.