
【题目】已知等腰梯形![]() 中(如图1),
中(如图1),![]() ,
, ![]() ,
, ![]() 为线段
为线段![]() 的中点,
的中点, ![]() 为线段
为线段![]() 上的点,
上的点, ![]() ,现将四边形
,现将四边形![]() 沿
沿![]() 折起(如图2).
折起(如图2).
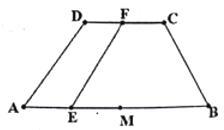
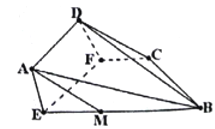
图1 图2
⑴求证: ![]() 平面
平面![]() ;
;
⑵在图2中,若![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)连接![]() ,由
,由![]() 可得
可得![]() ,即可证
,即可证![]() ∥
∥![]() 且
且![]() ,然后即可证出四边形
,然后即可证出四边形![]() 为平行四边形,进而可证明
为平行四边形,进而可证明![]() 平面
平面![]() ;(2)作
;(2)作![]() 于
于![]() ,连接
,连接![]() ,在
,在![]() 中,可得
中,可得![]() ,在
,在![]() 中,可得
中,可得![]() ,结合
,结合![]() ,推出
,推出![]() ,再由
,再由![]() ,推出
,推出![]() 平面
平面![]() ,即可得到
,即可得到![]() 为
为![]() 与平面
与平面![]() 所成的角,再根据余弦定理得出
所成的角,再根据余弦定理得出![]() ,进而可求出
,进而可求出![]() 的值,即直线
的值,即直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
试题解析:(1)证明:连接![]()
∵![]()
∴![]()
∴![]() ∥
∥![]() ,且
,且![]()
又∵![]() ∥
∥![]() ,且
,且![]()
∴![]() ∥
∥![]() ,且
,且![]()
∴四边形![]() 为平行四边形
为平行四边形
∴![]() ∥
∥![]()
又∵![]() 面
面![]() ,
, ![]() 面
面![]()
∴![]() ∥面
∥面![]()
(2)作![]() 于
于![]() ,连接
,连接![]() ,在
,在![]() 中,易知
中,易知![]() ,而
,而![]()
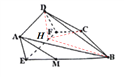
∴![]() ,
, ![]()
在![]() 中,
中, ![]() ,易知
,易知![]()
又∵![]()
∴![]()
在![]() 中,
中, ![]() ,
, ![]() ,
, ![]()
∴![]()
∴![]()
又∵![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() 平面
平面![]()
∴![]() 为
为![]() 在平面
在平面![]() 内的射影
内的射影
∴![]() 为
为![]() 与平面
与平面![]() 所成的角
所成的角
在![]() 中,易知
中,易知![]()
∴![]()
在![]() 中,
中, ![]()
∴![]() ,即
,即![]() 与平面
与平面![]() 的所成的角的正弦值为
的所成的角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,底面是等腰直角三角形,
中,底面是等腰直角三角形, ![]() ,侧棱
,侧棱![]() ,点
,点![]() 分别为棱
分别为棱![]() 的中点,
的中点, ![]() 的重心为
的重心为![]() ,直线
,直线![]() 垂直于平面
垂直于平面![]() .
.
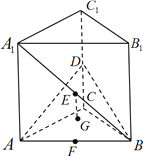
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦.
的余弦.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.
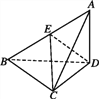
(1)求证:平面ABC⊥平面ACD;
(2)若E为AB中点,求点A到平面CED的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在圆
在圆![]() 上,
上, ![]() 的坐标分别为
的坐标分别为![]() ,
, ![]() ,线段
,线段![]() 的垂直平分线交线段
的垂直平分线交线段![]() 于点
于点![]()
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设圆![]() 与点
与点![]() 的轨迹
的轨迹![]() 交于不同的四个点
交于不同的四个点![]() ,求四边形
,求四边形![]() 的面积的最大值及相应的四个点的坐标.
的面积的最大值及相应的四个点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市垃圾处理站每月的垃圾处理量最少为400吨,最多为600吨,月处理成本![]() (元)与月垃圾处理量
(元)与月垃圾处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理一吨垃圾得到可利用的资源值为100元.
,且每处理一吨垃圾得到可利用的资源值为100元.
(1)该站每月垃圾处理量为多少吨时,才能使每吨垃圾的平均处理成本最低?
(2)该站每月能否获利?如果获利,求出最大利润;如果不获利,则需要市财政补贴,至少补贴多少元才能使该站不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E-ABCD中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(I)求棱锥C-ADE的体积;
(II)求证:平面ACE⊥平面CDE;
(III)在线段DE上是否存在一点F,使AF∥平面BCE?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数,
为常数, ![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,判断方程
时,判断方程![]() 是否有实根?若无实根请说明理由,若有实根请给出根的个数.
是否有实根?若无实根请说明理由,若有实根请给出根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() (
(![]() ,
, ![]() 为常数).
为常数).
(1)判断曲线![]() 的形状;
的形状;
(2)设曲线![]() 分别与
分别与![]() 轴,
轴, ![]() 轴交于点
轴交于点![]() ,
, ![]() (
(![]() ,
, ![]() 不同于原点
不同于原点![]() ),试判断
),试判断![]() 的面积
的面积![]() 是否为定值?并证明你的判断;
是否为定值?并证明你的判断;
(3)设直线![]() :
: ![]() 与曲线
与曲线![]() 交于不同的两点
交于不同的两点![]() ,
, ![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com