
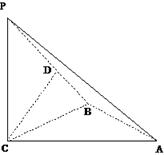
如图,三棱锥P—ABC中, PC![]() 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD![]() 平面PAB.
平面PAB.
(I) 求证:AB![]() 平面PCB;
平面PCB;
(II) 求异面直线AP与BC所成角的大小;
(III)求二面角C-PA-B的大小.
(1)证明见解析(2) ![]() (3) arcsin
(3) arcsin![]()
解法一:(I) ∵PC![]() 平面ABC,
平面ABC,![]() 平面ABC,
平面ABC,
∴PC![]() AB.…………………………2分
AB.…………………………2分
∵CD![]() 平面PAB,
平面PAB,![]() 平面PAB,
平面PAB,
∴CD![]() AB.…………………………4分
AB.…………………………4分
又![]() ,
,
∴AB![]() 平面PCB. …………………………5分
平面PCB. …………………………5分

(II) 过点A作AF//BC,且AF=BC,连结PF,CF.
则![]() 为异面直线PA与BC所成的角.………6分
为异面直线PA与BC所成的角.………6分
由(Ⅰ)可得AB⊥BC,
∴CF![]() AF.
AF.
由三垂线定理,得PF![]() AF.
AF.
则AF=CF=![]() ,PF=
,PF=![]() ,
,
在![]() 中, tan∠PAF=
中, tan∠PAF=![]() =
=![]() ,
,
∴异面直线PA与BC所成的角为![]() .…………………………………9分
.…………………………………9分
(III)取AP的中点E,连结CE、DE.
∵PC=AC=2,∴CE ![]() PA,CE=
PA,CE=![]() .
.
∵CD![]() 平面PAB,
平面PAB,
由三垂线定理的逆定理,得 DE ![]() PA.
PA.
∴![]() 为二面角C-PA-B的平面角.…………………………………11分
为二面角C-PA-B的平面角.…………………………………11分
由(I) AB![]() 平面PCB,又∵AB=BC,可求得BC=
平面PCB,又∵AB=BC,可求得BC=![]() .
.
在![]() 中,PB=
中,PB=![]() ,
,
![]() .
.
在![]() 中, sin∠CED=
中, sin∠CED=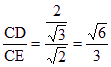 .
.
∴二面角C-PA-B的大小为arcsin![]() .……14分
.……14分
解法二:(I)同解法一.
(II) 由(I) AB![]() 平面PCB,∵PC=AC=2,
平面PCB,∵PC=AC=2,
又∵AB=BC,可求得BC=![]() .
.
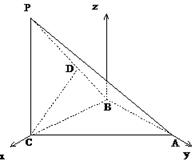
以B为原点,如图建立坐标系.
则A(0,![]() ,0),B(0,0,0),
,0),B(0,0,0),
C(![]() ,0,0),P(
,0,0),P(![]() ,0,2).
,0,2).
![]() ,
,![]() .
.
…………………7分
则![]() +0+0=2.
+0+0=2.
 =
=![]() =
= ![]() .
.
∴异面直线AP与BC所成的角为![]() .………………………10分
.………………………10分
(III)设平面PAB的法向量为m= (x,y,z).
![]() ,
,![]() ,
,
则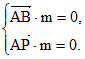 即
即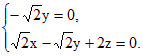
![]()
解得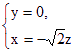 令
令![]() = -1, 得 m= (
= -1, 得 m= (![]() ,0,-1).
,0,-1).
设平面PAC的法向量为n=(![]() ).
).
![]() ,
,![]() ,
,
则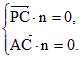 即
即
解得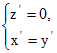 令
令![]() =1, 得 n= (1,1,0).……………………………12分
=1, 得 n= (1,1,0).……………………………12分
![]() =
=![]() .
.
∴二面角C-PA-B的大小为arccos![]() .………………………………14分
.………………………………14分


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
 如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB
如图,三棱锥P-ABC中,PC⊥平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD⊥平面PAB查看答案和解析>>
科目:高中数学 来源: 题型:
 (2006•石景山区一模)如图,三棱锥P-ABC中,
(2006•石景山区一模)如图,三棱锥P-ABC中,| PA |
| AB |
| PA |
| AC |
| AB |
| AC |
| PA |
| AC |
| AB |
|
| ||
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2
(2012•湖南模拟)如图,三棱锥P-ABC中,侧面PAC⊥底面ABC,∠APC=90°,且AB=4,AP=PC=2,BC=2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为
(2012•德阳二模)如图,三棱锥P-ABC中,PA丄面ABC,∠ABC=90°,PA=AB=1,BC=2,则P-ABC的外接球的表面积为查看答案和解析>>
科目:高中数学 来源: 题型:
 如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,AB=2
如图在三棱锥P-ABC中,AB⊥PC,AC=2,BC=4,AB=2| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com