
【题目】如图是2019年11月1日到11月20日,某地区甲流疫情新增数据的走势图.
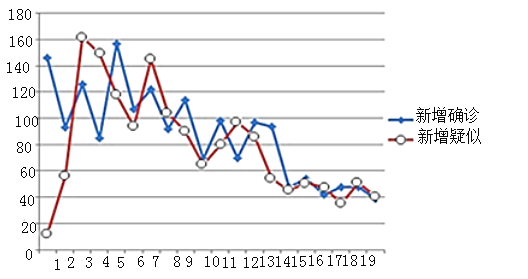
(1)从这20天中任选1天,求新增确诊和新增疑似的人数都超过100的概率;
(2)从新增确诊的人数超过100的日期中任选两天,用X表示新增确诊的人数超过140的天数,求X的分布列和数学期望;
(3)根据这20天统计数据,预测今后该地区甲流疫情的发展趋势.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() ;(3)见解析
;(3)见解析
【解析】
(1)根据走势图新增确诊和新增疑似人数超过100人的有3天,从而根据随机事件的概率公式,得到答案;
(2)根据题意得到X的所有可能值为0,1,2,从而得到相应的概率;
(3)基于图表的数据,预测今后该地区甲流疫情的发展趋势.
(1)由图知,在统计出的20天中,
新增确诊和新增疑似人数超过100人的有3天,
设事件![]() 为“从这20天中任取1天,新增确诊和新增疑似的人数都超过100”,
为“从这20天中任取1天,新增确诊和新增疑似的人数都超过100”,
则![]() .
.
(2)由图知,新增确诊的日期中人数超过100的有6天中,有2天人数超过140,
所以X的所有可能值为0,1,2.
所以![]() ,
,
![]() ,
,
![]() .
.
所以X的分布列为
X | 0 | 1 | 2 |
P |
|
|
|
所以![]() 的数学期望为
的数学期望为![]() .
.
(3)预测一:新增确诊和新增疑似的人数逐渐减少.
预测二:新增确诊和新增疑似的人数每天大致相当.
预测三:该地区甲流疫情趋于减缓.
预测四:该地区甲流疫情持续走低,不会爆发.
(答案不唯一,只要结论是基于图表的数据得出的,都给分).


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的离心率为
的离心率为![]() ,以原点
,以原点![]() 为圆心,椭圆
为圆心,椭圆![]() 的长半轴为半径的圆与直线
的长半轴为半径的圆与直线![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,
, ![]() 为动直线
为动直线![]() 与椭圆
与椭圆![]() 的两个交点,问:在
的两个交点,问:在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 为定值?若存在,试求出点
为定值?若存在,试求出点![]() 的坐标和定值,若不存在,请说明理由.
的坐标和定值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 且
且![]() ).
).
(1)若![]() 的定义域为
的定义域为![]() ,判断
,判断![]() 的单调性,并加以说明;
的单调性,并加以说明;
(2)当![]() 时,是否存在
时,是否存在![]() ,
,![]() ,使得
,使得![]() 在区间
在区间![]() 上的值域为
上的值域为![]() ,若存在,求
,若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的各项均为正数,前
的各项均为正数,前![]() 项和
项和![]() 满足
满足![]() ;数列
;数列![]() 是等比数列,前
是等比数列,前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知等比数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 前
前![]() 项和为
项和为![]() ;
;
(3)若![]() ,且等比数列
,且等比数列![]() 的公比
的公比![]() ,若存在
,若存在![]() ,使得
,使得![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
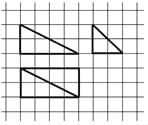
【题目】我国古代数学名著《九章算术商功》中阐述:“斜解立方,得两堑堵.斜解堑堵,其一为阳马,一为鳖臑.阳马居二,鳖臑居一,不易之率也.合两鳖臑三而一,验之以棊,其形露矣.”若称为“阳马”的某几何体的三视图如图所示,图中网格纸上小正方形的边长为1,对该几何体有如下描述:
①四个侧面都是直角三角形;
②最长的侧棱长为![]() ;
;
③四个侧面中有三个侧面是全等的直角三角形;
④外接球的表面积为24π.
其中正确的描述为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() (
(![]() )的焦点是椭圆
)的焦点是椭圆![]() :
: ![]() (
(![]() )的右焦点,且两曲线有公共点
)的右焦点,且两曲线有公共点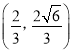
(1)求椭圆![]() 的方程;
的方程;
(2)椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,
, ![]() ,若过点
,若过点![]() 且斜率不为零的直线
且斜率不为零的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,已知直线
两点,已知直线![]() 与
与![]() 相较于点
相较于点![]() ,试判断点
,试判断点![]() 是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
是否在一定直线上?若在,请求出定直线的方程;若不在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com