
【题目】11月,2019全国美丽乡村篮球大赛在中国农村改革的发源地-安徽凤阳举办,其间甲、乙两人轮流进行篮球定点投篮比赛(每人各投一次为一轮),在相同的条件下,每轮甲乙两人在同一位置,甲先投,每人投一次球,两人有1人命中,命中者得1分,未命中者得-1分;两人都命中或都未命中,两人均得0分,设甲每次投球命中的概率为![]() ,乙每次投球命中的概率为
,乙每次投球命中的概率为![]() ,且各次投球互不影响.
,且各次投球互不影响.
(1)经过1轮投球,记甲的得分为![]() ,求
,求![]() 的分布列;
的分布列;
(2)若经过![]() 轮投球,用
轮投球,用![]() 表示经过第
表示经过第![]() 轮投球,累计得分,甲的得分高于乙的得分的概率.
轮投球,累计得分,甲的得分高于乙的得分的概率.
①求![]() ;
;
②规定![]() ,经过计算机计算可估计得
,经过计算机计算可估计得![]() ,请根据①中
,请根据①中![]() 的值分别写出a,c关于b的表达式,并由此求出数列
的值分别写出a,c关于b的表达式,并由此求出数列![]() 的通项公式.
的通项公式.
【答案】(1)分布列见解析;(2)①![]() ;②
;②![]() ,
,![]() .
.
【解析】
(1)经过1轮投球,甲的得分![]() 的取值为
的取值为![]() ,记一轮投球,甲投中为事件
,记一轮投球,甲投中为事件![]() ,乙投中为事件
,乙投中为事件![]() ,
,![]() 相互独立,计算概率后可得分布列;
相互独立,计算概率后可得分布列;
(2)由(1)得![]() ,由两轮的得分可计算出
,由两轮的得分可计算出![]() ,计算
,计算![]() 时可先计算出经过2轮后甲的得分
时可先计算出经过2轮后甲的得分![]() 的分布列(
的分布列(![]() 的取值为
的取值为![]() ),然后结合
),然后结合![]() 的分布列和
的分布列和![]() 的分布可计算
的分布可计算![]() ,
,
由![]() ,代入
,代入![]() ,得两个方程,解得
,得两个方程,解得![]() ,从而得到数列
,从而得到数列![]() 的递推式,变形后得
的递推式,变形后得![]() 是等比数列,由等比数列通项公式得
是等比数列,由等比数列通项公式得![]() ,然后用累加法可求得
,然后用累加法可求得![]() .
.
(1)记一轮投球,甲命中为事件![]() ,乙命中为事件
,乙命中为事件![]() ,
,![]() 相互独立,由题意
相互独立,由题意![]() ,
,![]() ,甲的得分
,甲的得分![]() 的取值为
的取值为![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
![]() ,
,
∴![]() 的分布列为:
的分布列为:
| -1 | 0 | 1 |
|
|
|
|
(2)由(1)![]() ,
,
![]()
![]() ,
,
同理,经过2轮投球,甲的得分![]() 取值
取值![]() :
:
记![]() ,
,![]() ,
,![]() ,则
,则
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
由此得甲的得分![]() 的分布列为:
的分布列为:
| -2 | -1 | 0 | 1 | 2 |
|
|
|
|
|
|
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴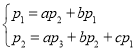 ,
,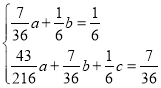 ,∴
,∴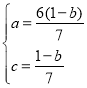 ,
,
代入![]() 得:
得:![]() ,
,
∴![]() ,
,
∴数列![]() 是等比数列,公比为
是等比数列,公比为![]() ,首项为
,首项为![]() ,
,
∴![]() .
.
∴![]()
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】平行志愿投档录取模式是高考志愿的一种新方式,2008年教育部在6个省区实行平行志愿投档录取模式的试点改革.一年的实践证叨,实行平行志愿投档录取模式,有效降低了考生志愿填报风险.平行志愿是这样规定:在同一批次设置几个志愿,当考生分数达到这几个学校提档线时,本批次的志愿依次检索录取.某考生根据对自己的高考分数和对往年学校录取情况分析,从报考指南中选择了10所学校,作出如下表格:
学校 |
|
|
|
|
|
|
|
|
|
|
专业 | 数学系 | 计算机系 | 物理系 | |||||||
录取概率 | 0.5 | 0.5 | 0.6 | 0.9 | 0.5 | 0.7 | 0.8 | 0.7 | 0.8 | 0.9 |
(1)该考生从上表中的10所学校中选择4所学校填报,记![]() 为选择的4所学校中报数学系专业的个数,求
为选择的4所学校中报数学系专业的个数,求![]() 的分布列及其期望
的分布列及其期望![]() ;
;
(2)若该考生选择了![]() 、
、![]() 、
、![]() 、
、![]() 这4个学校在同一批次填报志愿,填报志愿表如下,如果仅以该考生对自己分析的录取概率为依据,当改变这4个志愿填报的顺序时,是否改变他本批次录取的可能性?请说明理由.
这4个学校在同一批次填报志愿,填报志愿表如下,如果仅以该考生对自己分析的录取概率为依据,当改变这4个志愿填报的顺序时,是否改变他本批次录取的可能性?请说明理由.
志愿 | 学校 |
第一志愿 | |
第二志愿 | |
第三志愿 | |
第四志愿 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的离心率为
)的离心率为![]() ,点
,点![]() 在椭圆C上,直线
在椭圆C上,直线![]() 与椭圆C交于不同的两点A,B.
与椭圆C交于不同的两点A,B.
(1)求椭圆C的方程;
(2)直线![]() ,
,![]() 分别交y轴于M,N两点,问:x轴上是否存在点Q,使得
分别交y轴于M,N两点,问:x轴上是否存在点Q,使得![]() ?若存在,求出点Q的坐标;若不存在,请说明理由.
?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 在直线
在直线![]() 的左上方.
的左上方.
(1)若以![]() 为直径的圆恰好经过椭圆右焦点
为直径的圆恰好经过椭圆右焦点![]() ,求此时直线
,求此时直线![]() 的方程;
的方程;
(2)求证:![]() 的内切圆的圆心在定直线
的内切圆的圆心在定直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】检验中心为筛查某种疾病,需要检验血液是否为阳性,对![]() 份血液样本,有以下两种检验方式:①逐份检验,需要检验
份血液样本,有以下两种检验方式:①逐份检验,需要检验![]() 次;②混合检验,即将其中
次;②混合检验,即将其中![]() (
(![]() 且
且![]() )份血液样本分别取样混合在一起检验,若检验结果为阴性,这
)份血液样本分别取样混合在一起检验,若检验结果为阴性,这![]() 份的血液全为阴性,因而这
份的血液全为阴性,因而这![]() 份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这
份血液样本只要检验一次就够了,如果检验结果为阳性,为了明确这![]() 份血液究竟哪几份为阳性,再对这
份血液究竟哪几份为阳性,再对这![]() 份再逐份检验,此时这
份再逐份检验,此时这![]() 份血液的检验次数总共为
份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阳性还是阴性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份样本为阳性,若采用逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中![]() (
(![]() 且
且![]() )份血液样本,记采用逐份检验方式,样本需要检验的总次数为
)份血液样本,记采用逐份检验方式,样本需要检验的总次数为![]() ,采用混合检验方式,样本需要检验的总次数为点
,采用混合检验方式,样本需要检验的总次数为点![]() .当
.当![]() 时,根据
时,根据![]() 和
和![]() 的期望值大小,讨论当
的期望值大小,讨论当![]() 取何值时,采用逐份检验方式好?
取何值时,采用逐份检验方式好?
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着运动app和手环的普及和应用,在朋友圈、运动圈中出现了每天1万步的健身打卡现象,“日行一万步,健康一辈子”的观念广泛流传.“健步达人”小王某天统计了他朋友圈中所有好友(共500人)的走路步数,并整理成下表:
分组(单位:千步) |
|
|
|
|
|
|
|
|
频数 | 60 | 240 | 100 | 60 | 20 | 18 | 0 | 2 |
(1)请估算这一天小王朋友圈中好友走路步数的平均数(同一组中数据以这组数据所在区间中点值作代表);
(2)若用![]() 表示事件“走路步数低于平均步数”,试估计事件
表示事件“走路步数低于平均步数”,试估计事件![]() 发生的概率;
发生的概率;
(3)若称每天走路不少于8千步的人为“健步达人”,小王朋友圈中岁数在40岁以上的中老年人共有300人,其中健步达人恰有150人,请填写下面![]() 列联表.根据列联表判断,有多大把握认为,健步达人与年龄有关?
列联表.根据列联表判断,有多大把握认为,健步达人与年龄有关?
健步达人 | 非健步达人 | 合计 | |
40岁以上 | |||
不超过40岁 | |||
合计 |
附: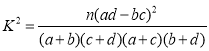 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com