
【题目】给定正整数![]() .将三种水果分装在
.将三种水果分装在![]() 个箱子中.试求最小的正整数
个箱子中.试求最小的正整数![]() ,使得无论水果如何分布,总可选出
,使得无论水果如何分布,总可选出![]() 个箱子,它们所装的三种水果都不少于各自总量的一半.
个箱子,它们所装的三种水果都不少于各自总量的一半.
【答案】![]()
【解析】
记三种水果为![]() 、
、![]() 、
、![]() ,
,![]() 表示第
表示第![]() 个箱子中所装的
个箱子中所装的![]() 水果的量.
水果的量.
考虑这样的分布:一只箱子装所有的![]() 水果,另一只箱子装所有的
水果,另一只箱子装所有的![]() 水果,其余
水果,其余![]() 只箱子平均装所有的
只箱子平均装所有的![]() 水果.
水果.
显然,![]() ,其中,
,其中,![]() 表示不超过实数
表示不超过实数![]() 的最大整数.
的最大整数.
下证:![]() 就是所求的最小值
就是所求的最小值
首先证明一个引理.
引理 ![]() 只箱子中装有
只箱子中装有![]() 、
、![]() 两种水果,单箱
两种水果,单箱![]() 水果的最大值为
水果的最大值为![]() ,
,![]() 水果的最大值为
水果的最大值为![]() 则可将所有的箱子分为
则可将所有的箱子分为![]() 、
、![]() 两组,每组
两组,每组![]() 只箱子,使得
只箱子,使得
![]() ,
,
![]() .
.
证明 设![]()
令![]() ,
,![]() .则
.则![]() .
.
假定已将![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 等分为
等分为![]() ,
,![]() ,
,
满足![]() .
.
不妨设![]() ,
,![]() 和
和![]() 中
中![]() 水果较少的为
水果较少的为![]() ,较多的为
,较多的为![]() .
.
令![]() ,
,![]()
则![]()
![]() .
.
依此,全部![]() 只箱子分为两组
只箱子分为两组
![]() ,
,![]() ,且
,且![]()
不妨设![]() .
.
注意到,由原来的排序知![]()
则 .
.
回到原题.
当![]() 为偶数时,设第1箱中
为偶数时,设第1箱中![]() 水果最多,余下的
水果最多,余下的![]() 箱中第2箱
箱中第2箱![]() 水果最多,另外
水果最多,另外![]() 箱依引理等分为
箱依引理等分为![]() 、
、![]() 两组.
两组.
设![]() .由
.由![]() ,
,![]()
知![]() 所装的三种水果都不少于各自总量的一半,且其箱子数为
所装的三种水果都不少于各自总量的一半,且其箱子数为![]() .
.
当![]() 为奇数时,先任取一箱,余下的
为奇数时,先任取一箱,余下的![]() 箱同上处理,共取出
箱同上处理,共取出![]() 箱,所装的三种水果都不少于各自总量的一半.
箱,所装的三种水果都不少于各自总量的一半.
因此,所求的![]() 在的最小值为
在的最小值为![]()


科目:高中数学 来源: 题型:
【题目】![]() 年上半年,随着新冠肺炎疫情在全球蔓延,全球超过
年上半年,随着新冠肺炎疫情在全球蔓延,全球超过![]() 个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为
个国家或地区宣布进人紧急状态,部分国家或地区直接宣布“封国”或“封城”,随着国外部分活动进入停摆,全球经济缺乏活力,一些企业开始倒闭,下表为![]() 年第一季度企业成立年限与倒闭分布情况统计表:
年第一季度企业成立年限与倒闭分布情况统计表:
企业成立年份 | 2019 | 2018 | 2017 | 2016 | 2015 |
企业成立年限 | 1 | 2 | 3 | 4 | 5 |
倒闭企业数量(万家) | 5.28 | 4.72 | 3.58 | 2.70 | 2.15 |
倒闭企业所占比例 | 21.4% | 19.1% | 14.5% | 10.9% | 8.7% |
(1)由所给数据可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程,预测
的回归方程,预测![]() 年成立的企业中倒闭企业所占比例.
年成立的企业中倒闭企业所占比例.
参考数据:![]() ,
,![]() ,
,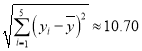 ,
,![]() ,
,
相关系数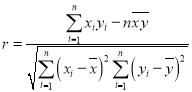 ,样本
,样本![]() 的最小二乘估计公式为
的最小二乘估计公式为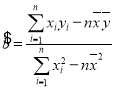 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有2013位来自不同国家的代表参加一个会议,每位代表都懂得若干种语言,已知其中任意四位代表之间都可进行交谈而不需要此四位代表以外的其他人帮助,即此四人中的任意两人都能讲同一种语言而实现直接沟通,或者通过第三个人的翻译实现间接沟通,或者通过他们各自的翻译能讲的同一种语言实现低效的间接沟通,证明:可以将所有代表分配住进671个房间,每个房间住3人,使得每个房间的3人都可以交谈。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为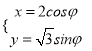 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求经过椭圆![]() 右焦点
右焦点![]() 且与直线
且与直线![]() 垂直的直线的极坐标方程;
垂直的直线的极坐标方程;
(2)若![]() 为椭圆
为椭圆![]() 上任意-点,当点
上任意-点,当点![]() 到直线
到直线![]() 距离最小时,求点
距离最小时,求点![]() 的直角坐标.
的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com