

 和此法向量夹角求解.向量知识求解.
和此法向量夹角求解.向量知识求解. 在此法向量方向上投影的绝对值.利用向量知识求解.
在此法向量方向上投影的绝对值.利用向量知识求解.
 ,0,a),C(0,a,0),B1 (a,a,a)
,0,a),C(0,a,0),B1 (a,a,a) =(-
=(- ,0,a),
,0,a), =(-a,a,0)----2分
=(-a,a,0)----2分 ,----------------------------------2分
,----------------------------------2分 ------------------------------1分
------------------------------1分 ,
,
 -------1分
-------1分
 ,
, -----3分
-----3分 =
= -----------------------------2分
-----------------------------2分

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
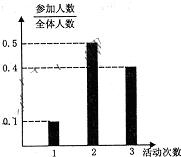 (理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.
(理科)某中学号召学生在2010年春节期间至少参加一次社会公益活动(下面简称为“活动”).该校合唱团共有100名学生,他们参加活动的次数统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
 (理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题:
(理科做)如图所示已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面ABCD且PA=1.建立适当的空间坐标系,利用空间向量求解下列问题:查看答案和解析>>
科目:高中数学 来源: 题型:
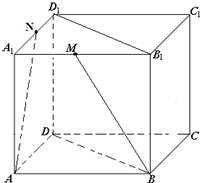 (理科)如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M是棱A1B1的中点,N是棱A1D1的中点.
(理科)如图所示,ABCD-A1B1C1D1是棱长为a的正方体,M是棱A1B1的中点,N是棱A1D1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com