
【题目】已知数列{an}的前n项和为Sn,且an=![]() (3n+Sn)对一切正整数n成立
(3n+Sn)对一切正整数n成立
(I)证明:数列{3+an}是等比数列,并求出数列{an}的通项公式;
(II)设![]() ,求数列
,求数列![]() 的前n项和Bn;
的前n项和Bn;
科目:高中数学 来源: 题型:
【题目】四棱锥P﹣ABCD中,AD![]() BC,BC⊥CD,BC=CD=2AD=2,PD=
BC,BC⊥CD,BC=CD=2AD=2,PD=![]() ,侧面PBC是等边三角形.
,侧面PBC是等边三角形.
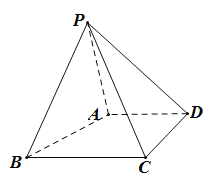
(1)证明:PA⊥平面PBC;
(2)求BC与平面PCD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)若点![]() 到直线
到直线![]() 的距离比它到点
的距离比它到点![]() 的距离小
的距离小![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
(2)设椭圆![]() 的离心率为
的离心率为![]() ,焦点在
,焦点在![]() 轴上且长轴长为
轴上且长轴长为![]() ,若曲线
,若曲线![]() 上的点到椭圆
上的点到椭圆![]() 的两个焦点的距离的差绝对值等于
的两个焦点的距离的差绝对值等于![]() ,求曲线
,求曲线![]() 的标准方程.
的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为招聘新员工设计了一个面试方案:应聘者从![]() 道备选题中一次性随机抽取
道备选题中一次性随机抽取![]() 道题,按照题目要求独立完成规定:至少正确完成其中
道题,按照题目要求独立完成规定:至少正确完成其中![]() 道题的便可通过.已知
道题的便可通过.已知![]() 道备选题中应聘者甲有
道备选题中应聘者甲有![]() 道题能正确完成,
道题能正确完成,![]() 道题不能完成;应聘者乙每题正确完成的概率都是
道题不能完成;应聘者乙每题正确完成的概率都是![]() ,且每题正确完成与否互不影响
,且每题正确完成与否互不影响
(1)分别求甲、乙两人正确完成面试题数的分布列,并计算其数学期望;
(2)请分析比较甲、乙两人谁的面试通过的可能性大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)3个人坐在有八个座位的一排椅子上,若每个人的左右两边都要有空位,则不同坐法的种数为多少?
(2)某高校现有10个保送上大学的名额分配给7所高中学校,若每所高中学校至少有1个名额,则名额分配的方法共有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,过底面是矩形的四棱锥FABCD的顶点F作EF∥AB,使AB=2EF,且平面ABFE⊥平面ABCD,若点G在CD上且满足DG=G![]() .
.

求证:(1)FG∥平面AED;
(2)平面DAF⊥平面BAF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点M,N分别为正方体ABCD﹣A1B1C1D1的棱AA1,BB1的中点,以正方体的六个面的中心为顶点构成一个八面体,若平面D1MNC1将该八面体分割成上、下两部分的体积分别为V1、V2,则![]() ( )
( )
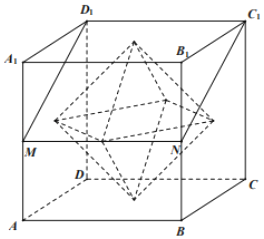
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com