
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,侧棱
是矩形,侧棱![]() 底面
底面![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
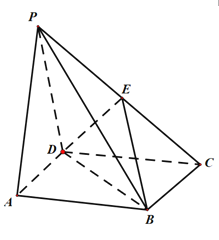
![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() 若直线
若直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的大小.
的大小.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节过后,某市教育局从全市高中生中抽去了100人,调查了他们的压岁钱收入情况,按照金额(单位:百元)分成了以下几组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .统计结果如下表所示:
.统计结果如下表所示:
![]()
该市高中生压岁钱收入![]() 可以认为服从正态分布
可以认为服从正态分布![]() ,用样本平均数
,用样本平均数![]() (每组数据取区间的中点值)作为
(每组数据取区间的中点值)作为![]() 的估计值.
的估计值.
(1)求样本平均数![]() ;
;
(2)求![]() ;
;
(3)某文化公司赞助了市教育局的这次社会调查活动,并针对该市的高中生制定了赠送“读书卡”的活动,赠送方式为:压岁钱低于![]() 的获赠两次读书卡,压岁钱不低于
的获赠两次读书卡,压岁钱不低于![]() 的获赠一次读书卡.已知每次赠送的读书卡张数及对应的概率如下表所示:
的获赠一次读书卡.已知每次赠送的读书卡张数及对应的概率如下表所示:

现从该市高中生中随机抽取一人,记![]() (单位:张)为该名高中生获赠的读书卡的张数,求
(单位:张)为该名高中生获赠的读书卡的张数,求![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国有一道古典数学名著——两鼠穿墙:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”题意是:“有两只老鼠从墙的两边打洞穿墙(连线与墙面垂直),大老鼠第一天进一尺,以后每天加倍,小老鼠第一天也进一尺,以后每天减半,那么两鼠第几天能见面.”假设墙厚16尺,如图是源于该题思想的一个程序框图,则输出的![]() ( )
( )
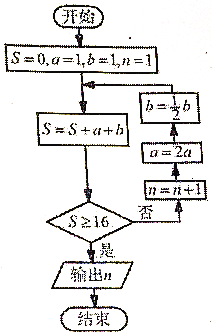
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的标准方程为
的标准方程为![]() ,圆心为
,圆心为![]() ,直线
,直线![]() 的方程为
的方程为![]() ,点
,点![]() 在直线
在直线![]() 上,过
上,过![]() 点作圆
点作圆![]() 的切线
的切线![]() ,
,![]() ,切点分别为
,切点分别为![]() ,
,![]() .
.
(1)若![]() ,试求点
,试求点![]() 的坐标;
的坐标;
(2)若![]() 点的坐标为
点的坐标为![]() ,过
,过![]() 作直线与圆
作直线与圆![]() 交于
交于![]() 两点,当
两点,当![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(3)求证:经过![]() ,
,![]() ,
,![]() 三点的圆必过定点,并求出所有定点的坐标.
三点的圆必过定点,并求出所有定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一名高二学生盼望2020年进入某名牌大学学习,假设该名牌大学有以下条件之一均可录取:①2020年2月通过考试进入国家数学奥赛集训队(集训队从2019年10月省数学竞赛一等奖中选拔):②2020年3月自主招生考试通过并且达到2020年6月高考重点分数线,③2020年6月高考达到该校录取分数线(该校录取分数线高于重点线),该学生具备参加省数学竞赛、自主招生和高考的资格且估计自己通过各种考试的概率如下表
省数学竞赛一等奖 | 自主招生通过 | 高考达重点线 | 高考达该校分数线 |
0.5 | 0.6 | 0.9 | 0.7 |
若该学生数学竞赛获省一等奖,则该学生估计进入国家集训队的概率是0.2.若进入国家集训队,则提前录取,若未被录取,则再按②、③顺序依次录取:前面已经被录取后,不得参加后面的考试或录取.(注:自主招生考试通过且高考达重点线才能录取)
(Ⅰ)求该学生参加自主招生考试的概率;
(Ⅱ)求该学生参加考试的次数![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)求该学生被该校录取的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5![]() ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设常数![]() .在平面直角坐标系
.在平面直角坐标系![]() 中,已知点
中,已知点![]() ,直线
,直线![]() :
:![]() ,曲线
,曲线![]() :
:![]() .
.![]() 与
与![]() 轴交于点
轴交于点![]() 、与
、与![]() 交于点
交于点![]() .
.![]() 、
、![]() 分别是曲线
分别是曲线![]() 与线段
与线段![]() 上的动点.
上的动点.
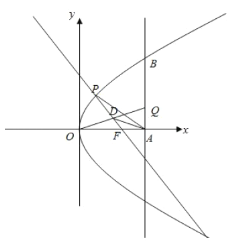
(1)用![]() 表示点
表示点![]() 到点
到点![]() 距离;
距离;
(2)设![]() ,
,![]() ,线段
,线段![]() 的中点在直线
的中点在直线![]() ,求
,求![]() 的面积;
的面积;
(3)设![]() ,是否存在以
,是否存在以![]() 、
、![]() 为邻边的矩形
为邻边的矩形![]() ,使得点
,使得点![]() 在
在![]() 上?若存在,求点
上?若存在,求点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com