
【题目】已知函数![]() .
.
(1)设![]() 是函数
是函数![]() 的极值点,求
的极值点,求![]() 的值,并求
的值,并求![]() 的单调区间;
的单调区间;
(2)若对任意![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源: 题型:
【题目】唐代诗人李欣的是![]() 古从军行
古从军行![]() 开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为
开头两句说“百日登山望烽火,黄昏饮马傍交河”诗中隐含着一个有缺的数学故事“将军饮马”的问题,即将军在观望烽火之后从山脚下某处出发,先到河边饮马后再回到军营,怎样走才能使总路程最短?在平面直角坐标系中,设军营所在区域为![]() ,若将军从
,若将军从![]() 出发,河岸线所在直线方程
出发,河岸线所在直线方程![]() ,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
,并假定将军只要到达军营所在区域即回到军营,则“将军饮马”的最短总路程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校需要从甲、乙两名学生中选一人参加数学竞赛,抽取了近期两人![]() 次数学考试的成绩,统计结果如下表:
次数学考试的成绩,统计结果如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成绩(分) |
|
|
|
|
|
乙的成绩(分) |
|
|
|
|
|
(1)若从甲、乙两人中选出一人参加数学竞赛,你认为选谁合适?请说明理由.
(2)若数学竞赛分初赛和复赛,在初赛中有两种答题方案:
方案一:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若答对,则可参加复赛,否则被淘汰.
道,若答对,则可参加复赛,否则被淘汰.
方案二:每人从![]() 道备选题中任意抽出
道备选题中任意抽出![]() 道,若至少答对其中
道,若至少答对其中![]() 道,则可参加复赛,否则被润汰.
道,则可参加复赛,否则被润汰.
已知学生甲、乙都只会![]() 道备选题中的
道备选题中的![]() 道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
道,那么你推荐的选手选择哪种答题方条进人复赛的可能性更大?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,点
中,点![]() 是底面
是底面![]() 的中心,
的中心,![]() 是线段
是线段![]() 的上一点。
的上一点。

(1)若![]() 为
为![]() 的中点,求直线
的中点,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)能否存在点![]() 使得平面
使得平面![]() 平面
平面![]() ,若能,请指出点
,若能,请指出点![]() 的位置关系,并加以证明;若不能,请说明理由。
的位置关系,并加以证明;若不能,请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确命题的序号是( )
①函数f(x)在定义域R内可导,“f′(1)=0”是“函数f(x)在x=1处取极值”的充分不必要条件;
②函数f(x)=x3![]() ax在[1,2]上单调递增,则a≥﹣4
ax在[1,2]上单调递增,则a≥﹣4
③在一次射箭比赛中,甲、乙两名射箭手各射箭一次.设命题p:“甲射中十环”,命题q:“乙射中十环”,则命题“至少有一名射箭手没有射中十环”可表示为(¬p)∨(¬q);
④若椭圆![]() 左、右焦点分别为F1,F2,垂直于x轴的直线交椭圆于A,B两点,当直线过右焦点时,△ABF1的周长取最大值
左、右焦点分别为F1,F2,垂直于x轴的直线交椭圆于A,B两点,当直线过右焦点时,△ABF1的周长取最大值
A.①③④B.②③④C.②③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
②“![]() ”是“函数
”是“函数![]() 在区间
在区间![]() 上为增函数”的充分不必要条件
上为增函数”的充分不必要条件
③若![]() 为假命题,则
为假命题,则![]() ,
,![]() 均为假命题
均为假命题
④对于命题![]() :
:![]() ,
,![]() ,则
,则![]() 为:
为:![]() ,
,![]()
其中真命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
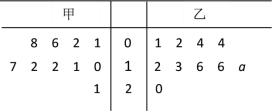
【题目】为培养学生的阅读习惯,某校开展了为期一年的“弘扬传统文化,阅读经典名著”活动. 活动后,为了解阅读情况,学校统计了甲、乙两组各10名学生的阅读量(单位:本),统计结果用茎叶图记录如下,乙组记录中有一个数据模糊,无法确认,在图中以a表示.
(Ⅰ)若甲组阅读量的平均值大于乙组阅读量的平均值, 求图中a的所有可能取值;
(Ⅱ)将甲、乙两组中阅读量超过15本的学生称为“阅读达人”. 设![]() ,现从所有“阅读达人”里任取3人,求其中乙组的人数X的分布列和数学期望.
,现从所有“阅读达人”里任取3人,求其中乙组的人数X的分布列和数学期望.
(Ⅲ)记甲组阅读量的方差为![]() . 在甲组中增加一名学生A得到新的甲组,若A的阅读量为10,则记新甲组阅读量的方差为
. 在甲组中增加一名学生A得到新的甲组,若A的阅读量为10,则记新甲组阅读量的方差为![]() ;若A的阅读量为20,则记新甲组阅读量的方差为
;若A的阅读量为20,则记新甲组阅读量的方差为![]() ,试比较
,试比较![]() ,
,![]() ,
,![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com