
【题目】在平面直角坐标系xOy中,直线l的参数方程为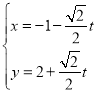 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为![]() ,曲线C2的直角坐标方程为
,曲线C2的直角坐标方程为![]() .
.
(1)若直线l与曲线C1交于M、N两点,求线段MN的长度;
(2)若直线l与x轴,y轴分别交于A、B两点,点P在曲线C2上,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)将直线l的参数方程消去参数,得到直角坐标方程,将圆C1的极坐标方程,转化为直角坐标方程,然后利用“r,d”法求弦长.
(2)将曲线C2的直角坐标方程转换为参数方程为![]() (0≤θ≤π),由A(1,0),B(0,1),P(2cosθ,2sinθ),得到
(0≤θ≤π),由A(1,0),B(0,1),P(2cosθ,2sinθ),得到![]() ,
,![]() 的坐标,再利用数量积公式得到
的坐标,再利用数量积公式得到![]()
![]() ,然后用正弦函数的性质求解.
,然后用正弦函数的性质求解.
(1)直线l的参数方程为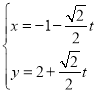 (t为参数),消去参数,
(t为参数),消去参数,
得直角坐标方程为x+y﹣1=0,
因为曲线C1的极坐标方程为![]() ,
,
所以![]()
所以直角坐标方程为x2+y2﹣2x+2y=0,
标准式方程为(x﹣1)2+(y+1)2=2,
所以圆心(1,﹣1)到直线x+y﹣1=0的距离d![]() ,
,
所以弦长|MN|=2![]() .
.
(2)因为曲线C2的直角坐标方程为![]() .
.
所以x2+y2=4![]() ,转换为参数方程为
,转换为参数方程为![]() (0≤θ≤π).
(0≤θ≤π).
因为A(1,0),B(0,1),点P在曲线C2上,故P(2cosθ,2sinθ),
所以![]() ,
,![]() ,(0≤θ≤π),
,(0≤θ≤π),
所以![]()
![]()
![]() ,
,
因为![]()
所以![]() ,
,
所以![]() .
.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
【题目】下列说法:
①分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 越大,说明“
越大,说明“![]() 与
与![]() 有关系”的可信度越大;
有关系”的可信度越大;
②以模型![]() 去拟合一组数据时,为了求出回归方程,设
去拟合一组数据时,为了求出回归方程,设![]() ,将其变换后得到线性方程
,将其变换后得到线性方程![]() ,则
,则![]() ,
,![]() 的值分别是
的值分别是![]() 和
和![]() ;
;
③在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
④若变量![]() 和
和![]() 满足关系
满足关系![]() ,且变量
,且变量![]() 与
与![]() 正相关,则
正相关,则![]() 与
与![]() 也正相关.
也正相关.
正确的个数是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() ,
,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)若函数![]() 在
在![]() 处的切线平行于
处的切线平行于![]() 轴,是否存在整数
轴,是否存在整数![]() ,使不等式
,使不等式![]() 在
在![]() 时恒成立?若存在,求出
时恒成立?若存在,求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大自然是非常奇妙的,比如蜜蜂建造的蜂房.蜂房的结构如图所示,开口为正六边形ABCDEF,侧棱AA'、BB'、CC'、DD'、EE'、FF'相互平行且与平面ABCDEF垂直,蜂房底部由三个全等的菱形构成.瑞士数学家克尼格利用微积分的方法证明了蜂房的这种结构是在相同容积下所用材料最省的,因此,有人说蜜蜂比人类更明白如何用数学方法设计自己的家园.英国数学家麦克劳林通过计算得到∠B′C′D′=109°28′16'.已知一个房中BB'=5![]() ,AB=2
,AB=2![]() ,tan54°44′08'
,tan54°44′08'![]() ,则此蜂房的表面积是_____.
,则此蜂房的表面积是_____.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甘肃省是土地荒漠化较为严重的省份,一代代治沙人为了固沙、治沙,改善生态环境,不断地进行研究与实践,实现了沙退人进.![]() 年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了
年,古浪县八步沙林场“六老汉”三代人治沙群体作为优秀代表,被中宣部授予“时代楷模”称号.在治沙过程中为检测某种固沙方法的效果,治沙人在某一实验沙丘的坡顶和坡腰各布设了![]() 个风蚀插钎,以测量风蚀值.(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为
个风蚀插钎,以测量风蚀值.(风蚀值是测量固沙效果的指标之一,数值越小表示该插钎处被风吹走的沙层厚度越小,说明固沙效果越好,数值为![]() 表示该插钎处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.
表示该插钎处没有被风蚀)通过一段时间的观测,治沙人记录了坡顶和坡腰全部插钎测得的风蚀值(所测数据均不为整数),并绘制了相应的频率分布直方图.
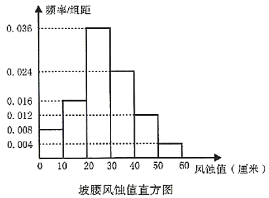
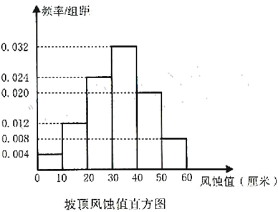
(Ⅰ)根据直方图估计“坡腰处一个插钎风蚀值小于![]() ”的概率;
”的概率;
(Ⅱ)若一个插钎的风蚀值小于![]() ,则该数据要标记“
,则该数据要标记“![]() ”,否则不标记根据以上直方图,完成列联表:
”,否则不标记根据以上直方图,完成列联表:
标记 | 不标记 | 合计 | |
坡腰 | |||
坡顶 | |||
合计 |
并判断是否有![]() 的把握认为数据标记“
的把握认为数据标记“![]() ”与沙丘上插钎所布设的位置有关?
”与沙丘上插钎所布设的位置有关?
附: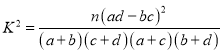 .
.
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)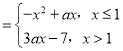 ,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
,若存在x1,x2∈R且x1≠x2,使得f(x1)=f(x2)成立,则实数a的取值范围是( )
A.[3,+∞)B.(3,+∞)C.(﹣∞,3)D.(﹣∞,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+acosx.
(1)求函数f(x)的奇偶性.并证明当|a|≤2时函数f(x)只有一个极值点;
(2)当a=π时,求f(x)的最小值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市房管局为了了解该市市民2018年1月至2019年1月期间购买二手房情况,首先随机抽样其中200名购房者,并对其购房面积![]() (单位:万元/平方米,
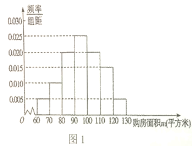
(单位:万元/平方米,![]() 进行了一次调查统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年1月至2019年1月期间当月在售二手房均价
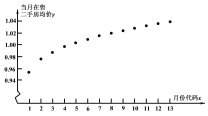
进行了一次调查统计,制成了如图1所示的频率分布直方图,接着调查了该市2018年1月至2019年1月期间当月在售二手房均价![]() (单位:万元平方米),制成了如图2所示的散点图(图中月份代码1-13分别对应2018年1月至2019年1月).
(单位:万元平方米),制成了如图2所示的散点图(图中月份代码1-13分别对应2018年1月至2019年1月).
(1)试估计该市市民的平均购房面积![]() .
.
(2)现采用分层抽样的方法从购房面积位于![]() 的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在
的40位市民中随机取4人,再从这4人中随机抽取2人,求这2人的购房面积恰好有一人在![]() 的概率.
的概率.
(3)根据散点图选![]() 和
和![]() 两个模型进行拟合,经过数据处理得到两个回归方程,分别为
两个模型进行拟合,经过数据处理得到两个回归方程,分别为![]() 和
和![]() ,并得到一些统计量的值,如下表所示:
,并得到一些统计量的值,如下表所示:
|
| |
| 0.000591 | 0.000164 |
| 0.00050 | |
请利用相关指数![]() 判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到0.001)./span>
判断哪个模型的拟合效果更好,并用拟合效果更好的模型预测2019年6月份的二手房购房均价(精确到0.001)./span>
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
参考公式: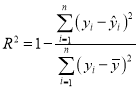 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com