Question

【题目】已知函数f（x）是定义域为R的偶函数，当时，f（x）=x2-2x

（1）求出函数f（x）在R上的解析式；

（2）画出函数f（x）的图象，并根据图象写出f（x）的单调区间．

（3）求使f（x）=1时的x的值．

Answer 1

【答案】（1）；（2）见解析；（3）

【解析】

(1) 设，则,根据函数为上的偶函数,当时，可得函数解析式；(2)根裾函数的解折式，利用描点法结合对称性可得函数的图象，利用函数的图象，可得函数的单谓区间；(3)结合的范围，分两种情况解方程可得到的值.

（1）当x＜0时，-x＞0，因为f（x）是偶函数，所以f（-x）=f（x）．

所以f（x）=f（-x）=x2+2x．

综上：f（x）=．

（2）图象如图所示．

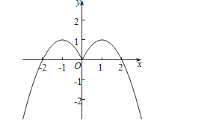
由图可知，单调增区间：[-1，0]，[1，+∞）

单调减区间：（-，-1）,(0,1)．

（3）当x＞0时，x2-2x=1

解得

因为x＞0，所以

当x＜0时，x2+2x=1，解得x=-1-或，

因为x＜0，所以x=-1-

综上所述，