
【题目】设函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)设![]() ,若对任意的
,若对任意的![]() ,存在
,存在![]() 使得
使得![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() .(2)
.(2)![]() 或
或![]() .
.
【解析】试题分析:(Ⅰ)由![]() ,得出
,得出![]() 的解析式,求切线方程,即先求
的解析式,求切线方程,即先求![]() 在
在![]() 处的值为切线的斜率,由点斜式求出切线方程即可;(Ⅱ)将题意等价于在区间
处的值为切线的斜率,由点斜式求出切线方程即可;(Ⅱ)将题意等价于在区间![]() 上,
上, ![]() 的最大值大于或等于
的最大值大于或等于![]() 的最大值”利用单调性可求出
的最大值”利用单调性可求出![]() 在
在![]() 上的最大值,在利用分类讨论的思想分为
上的最大值,在利用分类讨论的思想分为![]() ,
, ![]() ,
, ![]() 三种情形,求出其最大值,再进行比较即可.
三种情形,求出其最大值,再进行比较即可.
试题解析:解:(Ⅰ)当![]() 时,因为
时,因为![]() ,
,
所以![]() ,
, ![]() .
.
又因为![]() ,所以曲线
,所以曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,即
,即![]() .
.
(Ⅱ)“对任意的![]() ,存在
,存在![]() 使得
使得成立”等价于“在区间
![]() 上,
上, ![]() 的最大值大于或等于
的最大值大于或等于![]() 的最大值”.
的最大值”.
因为![]() ,所以
,所以![]() 在
在![]() 上的最大值为
上的最大值为![]() .
.
![]()
令![]() ,得
,得![]() 或
或![]() .
.
① 当![]() ,即
,即![]() 时,
时,
![]() 在
在![]() 上恒成立,
上恒成立,![]() 在
在![]() 上为单调递增函数,
上为单调递增函数,
![]() 的最大值为
的最大值为![]() ,
,
由![]() ,得
,得![]() .
.
② 当![]() ,即
,即![]() 时,
时,
当![]() 时,
时, ![]() ,
, ![]() 为单调递减函数,
为单调递减函数,
当![]() 时,
时, ![]() ,
, ![]() 为单调递增函数.
为单调递增函数.
所以![]() 的最大值为
的最大值为![]() 或
或![]() ,
,
由![]() ,得
,得![]() ;由
;由![]() ,得
,得![]() .
.
又因为![]() ,所以
,所以![]() .
.
③ 当![]() ,即
,即![]() 时,
时,
![]() 在
在![]() 上恒成立,
上恒成立, ![]() 在
在![]() 上为单调递减函数,
上为单调递减函数,
![]() 的最大值为
的最大值为![]() ,由
,由![]() ,得
,得![]() ,
,
又因为![]() ,所以
,所以![]() .
.
综上所述,实数![]() 的值范围是
的值范围是![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】质监部门从某超市销售的甲、乙两种食用油中分别各随机抽取100桶检测某项质量指标,由检测结果得到如下的频率分布直方图:
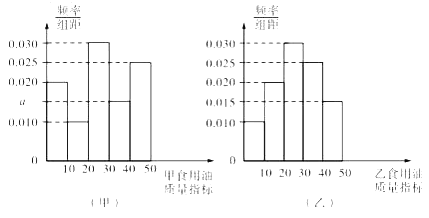
(Ⅰ)写出频率分布直方图(甲)中![]() 的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为
的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为![]() ,
,![]() ,试比较
,试比较![]() ,
,![]() 的大小(只要求写出答案);
的大小(只要求写出答案);
(Ⅱ)估计在甲、乙两种食用油中随机抽取1捅,恰有一桶的质量指标大于20;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,设
,设![]() 表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的桶数,求
表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的桶数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区问的中点值作代表,计算得![]()
②若![]()
![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知中心在坐标原点、焦点在x轴上的椭圆,它的离心率为![]() ,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
,且与直线x+y-1=0相交于M、N两点,若以MN为直径的圆经过坐标原点,求椭圆的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是奇函数,并且在R上为增函数,若0≤θ≤ ![]() 时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是( )
时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是( )
A.(0,1)
B.(﹣∞,0)
C.(﹣∞,1)
D.(﹣∞, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于![]() 维向量
维向量![]() ,若对任意
,若对任意![]() 均有
均有![]() 或
或![]() ,则称
,则称![]() 为
为![]() 维
维![]() 向量. 对于两个
向量. 对于两个![]() 维
维![]() 向量
向量![]() 定义
定义![]() .
.
(1)若![]() , 求
, 求![]() 的值;
的值;
(2)现有一个![]() 维
维![]() 向量序列:
向量序列: ![]() 若
若![]() 且满足:
且满足: ![]() ,求证:该序列中不存在
,求证:该序列中不存在![]() 维
维![]() 向量
向量![]() .
.
(3) 现有一个![]() 维
维![]() 向量序列:
向量序列: ![]() 若
若![]() 且满足:
且满足: ![]() ,若存在正整数
,若存在正整数![]() 使得
使得![]() 为
为![]() 维
维![]() 向量序列中的项,求出所有的
向量序列中的项,求出所有的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
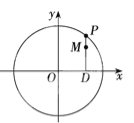
【题目】如图,设P是圆x2+y2=25上的动点,点D是P在x轴上的投影,M为PD上一点,且|MD|=![]() |PD|,当P在圆上运动时,求点M的轨迹C的方程。
|PD|,当P在圆上运动时,求点M的轨迹C的方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了制定治理学校门口上学、放学期间家长接送孩子乱停车现象的措施,对全校学生家长进行了问卷调查,根据从其中随机抽取的50份调查问卷,得到了如下的列联表.
同意限定区域停车 | 不同意限定区域停车 | 合计 | |
男 | 18 | 7 | 25 |
女 | 12 | 13 | 25 |
合计 | 30 | 20 | 50 |
(1)学校计划在同意限定区域停车的家长中,按照分层抽样的方法,随机抽取5人在上学、放学期间在学校门口参与维持秩序,在随机抽取的5人中,选出2人担任召集人,求至少有一名女性的概率?
(2)已知在同意限定区域停车的12位女性家长中,有3位日常开车接送孩子,现从这12位女性家长中随机抽取3人参与维持秩序,记参与维持秩序的女性家长中,日常开车接送孩子的女性家长人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设双曲线![]() 的上焦点为
的上焦点为![]() ,上顶点为
,上顶点为![]() ,点
,点![]() 为双曲线虚轴的左端点,已知
为双曲线虚轴的左端点,已知![]() 的离心率为
的离心率为![]() ,且
,且![]() 的面积
的面积![]() .
.

(1)求双曲线![]() 的方程;
的方程;
(2)设抛物线![]() 的顶点在坐标原点,焦点为
的顶点在坐标原点,焦点为![]() ,动直线
,动直线![]() 与
与![]() 相切于点
相切于点![]() ,与
,与![]() 的准线相交于点
的准线相交于点![]() ,试推断以线段
,试推断以线段![]() 为直径的圆是否恒经过
为直径的圆是否恒经过![]() 轴上的某个定点
轴上的某个定点![]() ?若是,求出定点
?若是,求出定点![]() 的坐标;若不是,请说明理由.
的坐标;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com