
【题目】对任意![]() ,给定区间
,给定区间![]() ,设函数
,设函数![]() 表示实数
表示实数![]() 与
与![]() 所属的给定区间内唯一整数之差的绝对值.
所属的给定区间内唯一整数之差的绝对值.
(1)当![]() 时,求出
时,求出![]() 的解析式;
的解析式;![]() 时,写出绝对值符号表示的
时,写出绝对值符号表示的![]() 解析式;
解析式;
(2)求![]() ,
,![]() ,判断函数
,判断函数![]() 的奇偶性,并证明你的结论;
的奇偶性,并证明你的结论;
(3)当![]() 时,求方程
时,求方程![]() 的实根.(要求说明理由,
的实根.(要求说明理由,![]() )
)
【答案】(1)![]() ,
,![]() ;
;![]() ,
,![]() ;(2)
;(2)![]() 是偶函数,证明见解析;(3)实根为
是偶函数,证明见解析;(3)实根为![]() .
.
【解析】
(1)可知区间![]() 中唯一整数为
中唯一整数为![]() ,根据定义可得出函数
,根据定义可得出函数![]() 在区间
在区间![]() 上的解析式,同理可得出函数
上的解析式,同理可得出函数![]() 在区间
在区间![]() 上的解析式;
上的解析式;
(2)根据题中定义求得![]() 和
和![]() 的值,可得出
的值,可得出![]() ,然后利用函数奇偶性的定义证明函数
,然后利用函数奇偶性的定义证明函数![]() 为偶函数,即可得出结论;
为偶函数,即可得出结论;
(3)要求方程![]() 的根,即求
的根,即求![]() 的根,对
的根,对![]() 分
分![]() 、
、![]() 、
、![]() 三种情况讨论,去绝对值符号,即可求得方程
三种情况讨论,去绝对值符号,即可求得方程![]() 根的个数.
根的个数.
(1)当![]() 时,
时,![]() 中唯一整数为
中唯一整数为![]() ,
,
由定义知![]() ,
,![]() .
.
当![]() 时,在
时,在![]() 中唯一整数为
中唯一整数为![]() ,
,
由定义知![]() ,
,![]() ;
;
(2)![]() ,
,![]() ,
,![]() ,
,![]() ,下面判断
,下面判断![]() 是偶函数.
是偶函数.
对任何![]() ,存在唯一
,存在唯一![]() ,使得
,使得![]() ,则
,则![]() ,
,
由![]() 可以得出
可以得出![]() ,
,
即![]() ,
,
由(1)的结论,![]() ,即函数
,即函数![]() 是偶函数;
是偶函数;
(3)![]() ,即
,即![]() ,其中
,其中![]() .
.
当![]() 时,
时,![]() ,所以方程
,所以方程![]() 没有大于
没有大于![]() 的实根;
的实根;
容易验证![]() 为方程
为方程![]() 的实根.
的实根.
当![]() 时对应的
时对应的![]() ,方程
,方程![]() 变为
变为![]() ,
,
设![]() ,
,
则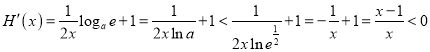 ,
,
故当![]() 时,函数
时,函数![]() 为减函数,
为减函数,![]() ,
,
方程![]() 没有满足
没有满足![]() 的实根;
的实根;
当![]() 时,对应的
时,对应的![]() ,方程
,方程![]() 变为
变为![]() ,
,
设![]() ,明显函数
,明显函数![]() 为减函数.
为减函数.
![]() ,
,
![]() ,则
,则![]() ,所以,
,所以,![]() ,
,
所以方程![]() 没有满足
没有满足![]() 的实根.
的实根.
综上,若![]() 时,方程
时,方程![]() 有且仅有一个实数根,实根为
有且仅有一个实数根,实根为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为4的菱形,∠BAD=60°,对角线AC与BD相交于点O,四边形ACFE为梯形,EF//AC,点E在平面ABCD上的射影为OA的中点,AE与平面ABCD所成角为45°.
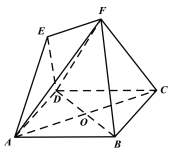
(Ⅰ)求证:BD⊥平面ACF;
(Ⅱ)求平面DEF与平面ABCD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一条曲线C在y轴右侧,曲线C上任意一点到点![]() 的距离减去它到y轴的距离都等于1.
的距离减去它到y轴的距离都等于1.
(1)求曲线C的方程;
(2)直线![]() 与轨迹C交于A,B两点,问:在x轴上是否存在定点
与轨迹C交于A,B两点,问:在x轴上是否存在定点![]() ,使得直线
,使得直线![]() 与
与![]() 关于x轴对称而与直线
关于x轴对称而与直线![]() 的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
的位置无关,若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )过点
)过点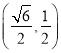 ,离心率为
,离心率为![]() .其左、右焦点分别为
.其左、右焦点分别为![]() ,
,![]() ,O为坐标原点.直线l:
,O为坐标原点.直线l:![]() 与以线段
与以线段![]() 为直径的圆相切,且直线l与椭圆C交于不同的A,B两点.
为直径的圆相切,且直线l与椭圆C交于不同的A,B两点.
(1)求椭圆C的方程;
(2)若满足![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的右焦点为
)的右焦点为![]() ,左右顶点分别为
,左右顶点分别为![]() 、
、![]() ,
,![]() ,过点
,过点![]() 的直线
的直线![]() (不与
(不与![]() 轴重合)交椭圆
轴重合)交椭圆![]() 于
于![]() 、
、![]() 点,直线
点,直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与直线
,与直线![]() 的交点为
的交点为![]() .
.
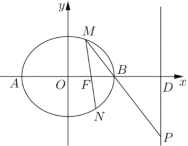
(1)求椭圆![]() 的方程;
的方程;
(2)若![]()
![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)求证:![]() 、
、![]() 、
、![]() 三点共线.
三点共线.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体ABCDEF满足:正方形ABCD与正三角形FBC所在的两个平面互相垂直,FB∥AE且FB=2EA.
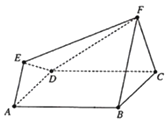
(1)证明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 是
是![]() 上一点.
上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 是
是![]() 分别关于两坐标轴及坐标原点的对称点,平行于
分别关于两坐标轴及坐标原点的对称点,平行于![]() 的直线
的直线![]() 交
交![]() 于异于
于异于![]() 的两点
的两点![]() .点
.点![]() 关于原点的对称点为
关于原点的对称点为![]() .证明:直线
.证明:直线![]() 与
与![]() 轴围成的三角形是等腰三角形.
轴围成的三角形是等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在测试中,客观题难题的计算公式为![]() ,其中
,其中![]() 为第
为第![]() 题的难度,
题的难度, ![]() 为答对该题的人数,
为答对该题的人数, ![]() 为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:
为参加测试的总人数.现对某校高三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如下表所示:

测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如下表所示(“√”表示答对,“×”表示答错):
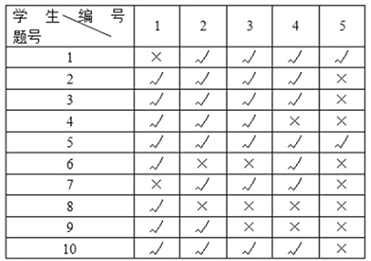
(1)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入下表,并估计这120名学生中第5题的实测答对人数;

(2)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(3)定义统计量![]() ,其中
,其中![]() 为第
为第![]() 题的实测难度,
题的实测难度, ![]() 为第
为第![]() 题的预估难度(
题的预估难度(![]() ).规定:若
).规定:若![]() ,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com