
【题目】如图,三棱锥S﹣ABC中,SA=SB=SC,∠ABC=90°,AB>BC,E,F,G分别是AB,BC,CA的中点,记直线SE与SF所成的角为α,直线SG与平面SAB所成的角为β,平面SEG与平面SBC所成的锐二面角为γ,则( )
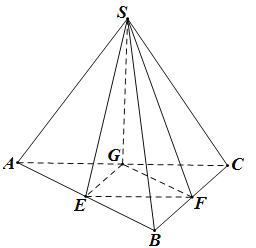
A.α>γ>βB.α>β>γC.γ>α>βD.γ>β>α
【答案】A
【解析】
根据题意可知,G作SE的垂线l,显然l垂直平面SAB,故直线SG与平面SAB所成的角为β=∠GSE,同理,平面SEG与平面SBC所成的锐二面角为γ=∠FSG,利用三角函数结合几何性质,得出结论.
因为AB⊥BC,SA=SB=SC,所以AB⊥SE,所以AB⊥平面SGE,AB⊥SG,
又SG⊥AC,所以SG⊥平面ABC,
过G作SE的垂线l,显然l垂直平面SAB,
故直线SG与平面SAB所成的角为β=∠GSE,
同理,平面SEG与平面SBC所成的锐二面角为γ=∠FSG,
由tanγ=![]() ,得γ>β,γ也是直线SF与平面SEG所成的角,
,得γ>β,γ也是直线SF与平面SEG所成的角,
由cosα=cosβcosγ<cosγ,则α>γ,所以α>γ>β,
故选:A.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
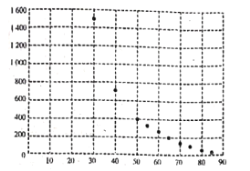
【题目】商品价格与商品需求量是经济学中的一种基本关系,某服装公司需对新上市的一款服装制定合理的价格,需要了解服装的单价x(单位:元)与月销量y(单位:件)和月利润z(单位:元)的影响,对试销10个月的价格![]() 和月销售量
和月销售量![]() (
(![]() )数据作了初步处理,得到如图所示的散点图及一些统计量的值.
)数据作了初步处理,得到如图所示的散点图及一些统计量的值.
x |
| y |
|
|
|
|
61 | 0.018 | 372 |
| 2670 | 26 | 0.0004 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为需求量y关于价格x的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为需求量y关于价格x的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立y关于x的回归方程;
(3)已知这批服装的成本为每件10元,根据(1)的结果回答下列问题;
(i)预测当服装价格![]() 时,月销售量的预报值是多少?
时,月销售量的预报值是多少?
(span>ii)当服装价格x为何值时,月利润的预报值最大?(参考数据![]() )
)
附:对于一组数据,其回归直线的斜率和截距的最小二乘估计分别为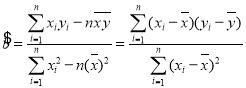 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的三边AB,BC,AC的长依次成等差数列,且|AB|>|AC|,B(-1,0),C(1,0),则顶点A的轨迹方程为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验“喜欢玩手机游戏与认为作业多”是否有关系,某班主任对班级的30名学生进行了调查,得到一个![]() 列联表:
列联表:
认为作业多 | 认为作业不多 | 合计 | |
喜欢玩手机游戏 | 18 | 2 | |
不喜欢玩手机游戏 | 6 | ||
合计 | 30 |
(1)请将上面的列联表补充完整(在答题卡上直接填写结果,不需要写求解过程);
(2)能否在犯错误的概率不超过0.005的前提下认为“喜欢玩手机游戏”与“认为作业多”有关系?
(3)若从不喜欢玩手机游戏的人中随机抽取3人,则至少2人认为作业不多的概率是多少?
参考公式及参考数据:独立性检验概率表
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
计算公式: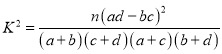
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:3x﹣4y+t=0,圆C1经过点A(0,1)与B(2,1),且被y轴的正半轴截得的线段长为2.
(1)求圆C1的方程;
(2)设圆C2是以直线l上的点为圆心的单位圆,若存在圆C2与圆C1有交点,求t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知棱长为1的正方体![]() 中,下列数学命题不正确的是( )
中,下列数学命题不正确的是( )
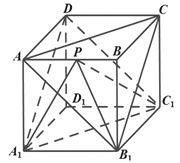
A.平面![]() 平面
平面![]() ,且两平面的距离为
,且两平面的距离为![]()
B.点![]() 在线段
在线段![]() 上运动,则四面体
上运动,则四面体![]() 的体积不变
的体积不变
C.与所有12条棱都相切的球的体积为![]()
D.![]() 是正方体的内切球的球面上任意一点,
是正方体的内切球的球面上任意一点,![]() 是
是![]() 外接圆的圆周上任意一点,则
外接圆的圆周上任意一点,则![]() 的最小值是
的最小值是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的列联表,且已知在甲、乙两个文科班全部110人中优秀的人数是30人.
(1)请完成上面的列联表;
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
参考公式与临界值表![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com