
【题目】如图①,正方形![]() 的边长为4,
的边长为4,![]() ,
,![]() ,把四边形
,把四边形![]() 沿
沿![]() 折起,使得
折起,使得![]() 平面
平面![]() ,
,![]() 是
是![]() 的中点,如图②
的中点,如图②
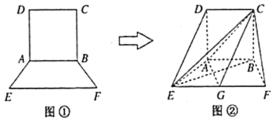
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]:在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (t为参数,
(t为参数,![]() ),以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为
),以坐标原点为极点,以x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() ,已知直线
,已知直线![]() 与曲线C交于不同的两点A,B.
与曲线C交于不同的两点A,B.
(1)求直线![]() 的普通方程和曲线C的直角坐标方程;
的普通方程和曲线C的直角坐标方程;
(2)设P(1,2),求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】目前,国内很多评价机构经过反复调研论证,研制出“增值评价”方式。下面实例是某市对“增值评价”的简单应用,该市教育评价部门对本市![]() 所高中按照分层抽样的方式抽出
所高中按照分层抽样的方式抽出![]() 所(其中,“重点高中”
所(其中,“重点高中”![]() 所分别记为
所分别记为![]() ,“普通高中”
,“普通高中”![]() 所分别记为
所分别记为![]() ),进行跟踪统计分析,将
),进行跟踪统计分析,将![]() 所高中新生进行了统的入学测试高考后,该市教育评价部门将人学测试成绩与高考成绩的各校平均总分绘制成了雷达图.
所高中新生进行了统的入学测试高考后,该市教育评价部门将人学测试成绩与高考成绩的各校平均总分绘制成了雷达图.![]() 点表示
点表示![]() 学校入学测试平均总分大约
学校入学测试平均总分大约![]() 分,
分,![]() 点表示
点表示![]() 学校高考平均总分大约
学校高考平均总分大约![]() 分,则下列叙述不正确的是( )
分,则下列叙述不正确的是( )

A.各校人学统一测试的成绩都在![]() 分以上
分以上
B.高考平均总分超过![]() 分的学校有
分的学校有![]() 所
所
C.![]() 学校成绩出现负增幅现象
学校成绩出现负增幅现象
D.“普通高中”学生成绩上升比较明显
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,上顶点为
,上顶点为![]() ,过
,过![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() .当
.当![]() 与
与![]() 重合时,
重合时,![]() 与
与![]() 的面积分别为
的面积分别为![]() 、
、![]() .
.
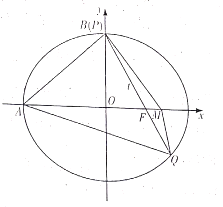
(1)求椭圆![]() 的方程;
的方程;
(2)在![]() 轴上找一点
轴上找一点![]() ,当
,当![]() 变化时,
变化时,![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,其中e为自然对数的底数).
,其中e为自然对数的底数).
(Ⅰ)若![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数![]() 有两个不同的零点
有两个不同的零点![]() .
.
(ⅰ)当![]() 时,求实数
时,求实数![]() 的取值范围;
的取值范围;
(ⅱ)设![]() 的导函数为
的导函数为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知原命题是“若![]() 则
则![]() ”.
”.
(1)试写出原命题的逆命题,否命题,逆否命题,并判断所写命题的真假;
(2)若“![]() ”是“
”是“![]() ”的必要不充分条件,求实数
”的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析的说法中错误的是( )
A.残差图中残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适
B.两个模型中残差平方和越小的模型拟合的效果越好
C.在线性回归方程![]() 中,当解释变量x每增加一个单位时,预报变量就平均增加0.2个单位
中,当解释变量x每增加一个单位时,预报变量就平均增加0.2个单位
D.甲、乙两个模型的![]() 分别约为0.98和0.80,则模型乙的拟合效果更好
分别约为0.98和0.80,则模型乙的拟合效果更好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com