
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为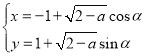 (
(![]() 为参数,
为参数,![]() ).
).
(Ⅰ)当![]() 时,若曲线
时,若曲线![]() 上存在
上存在![]() 两点关于点
两点关于点![]() 成中心对称,求直线
成中心对称,求直线![]() 的参数方程;
的参数方程;
(Ⅱ)在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,极坐标方程为
轴正半轴为极轴的极坐标系中,极坐标方程为![]() 的直线
的直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求实数
,求实数![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两企业生产同一种型号零件,按规定该型号零件的质量指标值落在![]() 内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
内为优质品.从两个企业生产的零件中各随机抽出了500件,测量这些零件的质量指标值,得结果如下表:
甲企业:

乙企业:

(1)已知甲企业的500件零件质量指标值的样本方差![]() ,该企业生产的零件质量指标值
,该企业生产的零件质量指标值![]() 服从正态分布
服从正态分布![]() ,其中
,其中![]() 近似为质量指标值的样本平均数
近似为质量指标值的样本平均数![]() (注:求
(注:求![]() 时,同一组数据用该区间的中点值作代表),
时,同一组数据用该区间的中点值作代表),![]() 近似为样本方差
近似为样本方差![]() ,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
,试根据该企业的抽样数据,估计所生产的零件中,质量指标值不低于71.92的产品的概率.(精确到0.001)
(2)由以上统计数据完成下面![]() 列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.
列联表,并问能否在犯错误的概率不超过0.01的前提下,认为“两个分厂生产的零件的质量有差异”.

附注:
参考数据: ![]() ,
,
参考公式: ![]() ,
, ![]() ,
,
![]() .
.
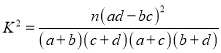
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
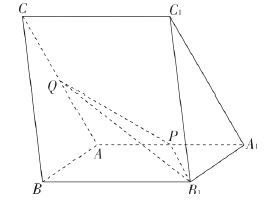
【题目】如图,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)在平面![]() 内过点
内过点![]() 作
作![]() 平面
平面![]() 交
交![]() 于点
于点![]() ,并写出作图步骤,但不要求证明.
,并写出作图步骤,但不要求证明.
(2)若侧面![]() 侧面
侧面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售![]() 件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为
件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为![]() ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为![]() ,记改进工艺后电子公司销售该配件的月平均利润是
,记改进工艺后电子公司销售该配件的月平均利润是![]() (元).
(元).
(1)写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x2﹣kx﹣4在区间[﹣2,4]上具有单调性,则k的取值范围是( )
A.[﹣8,16]
B.(﹣∞,﹣8]∪[16,+∞)
C.(﹣∞,﹣8)∪(16,+∞)
D.[16,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列每组函数是同一函数的是( )
A.f(x)=x0与f(x)=1
B.f(x)= ![]() ﹣1与f(x)=|x|﹣1
﹣1与f(x)=|x|﹣1
C.f(x)= ![]() 与f(x)=x﹣2
与f(x)=x﹣2
D.f(x)= ![]() 与f(x)=
与f(x)= ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() 恒等于常数
恒等于常数![]() ,则称
,则称![]() 具有局部等差数列
具有局部等差数列![]() .
.
(1)若![]() 具有局部等差数列
具有局部等差数列![]() ,且
,且![]()
![]() ,求
,求![]() ;
;
(2)若无穷数列![]() 是等差数列,无穷数列
是等差数列,无穷数列![]() 是公比为正数的等比数列,
是公比为正数的等比数列,![]() ,
,![]() ,
,![]() ,判断
,判断![]() 是否具有局部等差数列
是否具有局部等差数列![]() ,并说明理由;
,并说明理由;
(3)设![]() 既具有局部等差数列
既具有局部等差数列![]() ,又具有局部等差数列
,又具有局部等差数列![]() ,求证:
,求证:![]() 具有局部等差数列
具有局部等差数列![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com